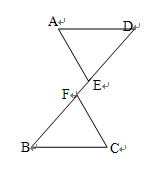
如图,已知平面直角坐标系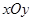 中,点
中,点 ,
,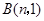 为两动点,其中
为两动点,其中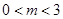 ,连结
,连结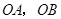 ,
,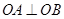 .
.
(1)求证: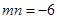 ;
;
(2)当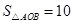 时,抛物线经过
时,抛物线经过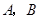 两点且以
两点且以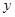 轴为对称轴,求抛物线对应的二次函数的关系式;
轴为对称轴,求抛物线对应的二次函数的关系式;
(3)在(2)的条件下,设直线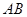 交
交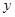 轴于点
轴于点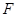 ,过点
,过点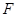 作直线
作直线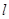 交抛物线于
交抛物线于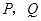 两点,问是否存在直线
两点,问是否存在直线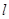 ,使
,使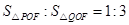 ?若存在,求出直线
?若存在,求出直线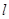 对应的函数关系式;若不存在,请说明理由.
对应的函数关系式;若不存在,请说明理由.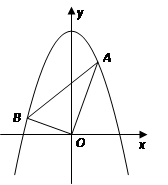
(1)如图①,已知C是线段AB上一点,分别以AC、BC为边长在AB的同侧作等边△ADC与等边△CBE,试猜想AE与DB的大小关系,并证明.
(2)如图②,当等边△CBE绕点C旋转后,上述结论是否仍成立?若成立,请证明;若不成立,请说明理由
如图,在△ABC中,D为BC的中点,DE⊥BC交∠BAC的平分线AE于E,EF⊥AB于F,EG⊥AC交AC延长线于G. 求证:BF=CG.
△ABC在平面直角坐标系中的位置如图所示: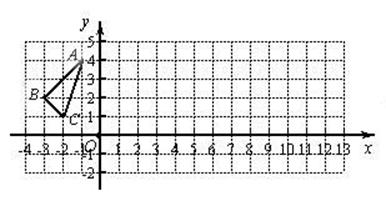
①作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
②将△ABC向右平移8个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
③观察△A1B1C1与△A2B2C2它们是否关于某直成对称?若是,请在图上画出这条对称轴.
如图,等边△ABC,∠1=∠2=∠3,求∠BEC的度数.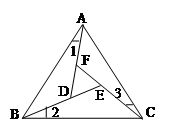
如图,E、F是线段BD上的两点,且DF=BE,AE=CF,AE∥CF.求证:AD∥BC.