有100名学生参加两次科技知识测试,条形图显示两次测试的分数分布情况.
请你根据条形图提供的信息,回答下列问题(把答案填在题中横线上);
(1)两次测试最低分在第 次测试中;
(2)第 次测试较容易;
(3)第一次测试中,中位数在 分数段,第二次测试中,中位数在 分数段.
已知,如图,O为正方形对角线的交点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG.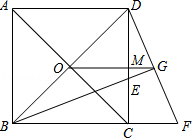
(1)求证:△BCE≌△DCF.
(2)判断OG与BF有什么关系,证明你的结论.
(3)若DF2=8-4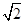 ,求正方形ABCD的面积?
,求正方形ABCD的面积?
物美商场于今年年初以每件25元的进价购进一批商品.当商品售价为40元时,一月份销售256件.二、三月该商品十分畅销.销售量持续走高.在售价不变的基础上,三月份的销售量达到400件.设二、三这两个月月平均增长率不变.
(1)求二、三这两个月的月平均增长率;
(2)从四月份起,商场采用降价促销的方式回馈顾客,经调查发现,该商品每降价1元,销售量增加5件,当商品降价多少元时,商场获利4250元?
已知,如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交与BE的延长线于点F,且AF=DC,连结CF.
(1)求证:四边形ADCF是平行四边形;
(2)当AB与AC有何数量关系时,四边形ADCF为矩形,请说明理由.
某市篮球队到市一中选拔一名队员.教练对王亮和李刚两名同学进行5次3分投篮测试,每人每次投10个球,下图记录的是这两名同学5次投篮中所投中的个数.
(1)请你根据图中的数据,填写下表;
| 姓名 |
平均数 |
众数 |
方差 |
| 王亮 |
7 |
||
| 李刚 |
7 |
2.8 |
(2)你认为谁的成绩比较稳定,为什么?
(3)若你是教练,你打算选谁?简要说明理由.
解方程:
(1)x2-3x+1=0;
(2)x(x+3)-(2x+6)=0.