某城市现有人口总数为100万人,如果年自然增长率为1.2%,试解答下列问题:
(1)写出该城市人口数y(万人)与年份x(年)的函数关系式;
(2)表示计算10年以后该城市人口总数的算法;
(3)用流程图表示计算大约多少年以后该城市人口将达到120万人的算法。
如图,四棱锥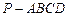 中,底面
中,底面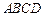 是平行四边形,
是平行四边形,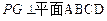 ,垂足为
,垂足为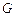 ,
,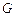 在
在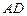 上,且
上,且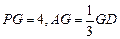 ,
,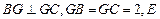 是
是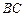 的中点.
的中点.
(1)求异面直线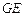 与
与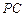 所成的角的余弦值;
所成的角的余弦值;
(2)若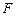 是棱
是棱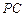 上一点,且
上一点,且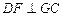 ,求
,求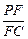 的值.
的值.
已知空间三点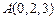 ,
,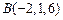 ,
,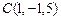
(1)求以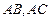 为边的平行四边形的面积;
为边的平行四边形的面积;
(2)若向量a分别与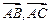 垂直,且|a|=
垂直,且|a|=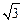 ,求a的坐标.
,求a的坐标.
设函数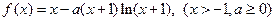 .
.
(1)求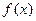 的单调区间;
的单调区间;
(2)当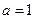 时,若方程
时,若方程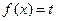 在
在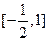 上有两个实数解,求实数t的取值范围;
上有两个实数解,求实数t的取值范围;
(3)证明:当m>n>0时,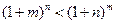 .
.
已知函数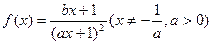 ,且
,且
(1)求函数 的表达式;
的表达式;
(2)若数列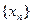 的项满足
的项满足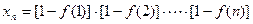 ,试求
,试求 ;
;
(3)猜想数列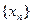 的通项,并用数学归纳法证明.
的通项,并用数学归纳法证明.
设函数f(x)=-x3+x2+(m2-1)x(x∈R),其中m>0.
(1)当m=1时,求曲线y=f(x)在点(1,f(1))处的切线的斜率;
(2)求函数f(x)的单调区间.