(本小题满分12分)
设命题p:函数 是R上的减函数,命题q: 函数
是R上的减函数,命题q: 函数 在
在 的值域是
的值域是 [-1,3].若“p且q”为假命题。“p或q” 为真命题,求
[-1,3].若“p且q”为假命题。“p或q” 为真命题,求 的取值范围
的取值范围
(本小题满分10分)设全集是实数集R ,集合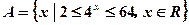 ,集合
,集合 ,
,
(1) 当  时 ,求
时 ,求 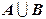 ;
;
(2) 若 ,求实数
,求实数 的取值范围.
的取值范围.
已知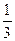 ≤
≤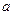 ≤1,若函数
≤1,若函数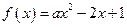 在区间[1,3]上的最大值
在区间[1,3]上的最大值
为 ,最小值为
,最小值为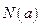 ,令
,令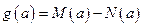 .
.
(1)求 的函数表达式;
的函数表达式;
(2)判断函数 在区间[
在区间[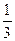 ,1]上的单调性,并求出
,1]上的单调性,并求出 的最小值 .
的最小值 .
某种商品在近30天内每件的销售价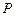 (元)与时间
(元)与时间 (天)的函数关系近似满足
(天)的函数关系近似满足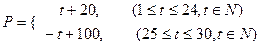 ,商品的日销售量
,商品的日销售量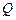 (件)与时间
(件)与时间 (天)的函数关系近似满足
(天)的函数关系近似满足 ,求这种商品日销售金额的最大值,并指出日销售金额最大的一天是30天中第几天?
,求这种商品日销售金额的最大值,并指出日销售金额最大的一天是30天中第几天?
设f(x)是定义在(0,+∞)上的增函数,且f( )=f(x)-f(y).
)=f(x)-f(y).
(1)求f(1)的值;
(2)若f(6)=1,解不等式f(x+5)-f(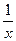 )<2.
)<2.