某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组 ,第2组
,第2组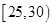 ,第3组
,第3组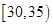 ,第4组
,第4组 ,第5组
,第5组 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
(2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
(本小题满分12分)
已知集合 ,
, ,(1)在区间
,(1)在区间 上任取一个实数
上任取一个实数 ,求“
,求“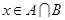 ”的概率;(2)设
”的概率;(2)设 为有序实数对,其中
为有序实数对,其中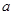 是从集合
是从集合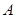 中任取的一个整数,
中任取的一个整数,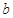 是从集合
是从集合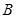 中任取的一个整数,求“
中任取的一个整数,求“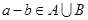 ”的概率.
”的概率.
(本小题满分7分)选修4-5:不等式选讲
已知实数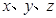 满足
满足 且
且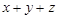 的最大值是7,求
的最大值是7,求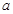 的值.
的值.
(本小题满分7分)选修4-4:坐标系与参数方程
已知曲线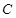 的极坐标方程是
的极坐标方程是 .以极点为平面直角坐标系的原点,极轴为
.以极点为平面直角坐标系的原点,极轴为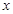 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线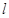 的参数方程是
的参数方程是 参数),点
参数),点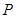 是曲线
是曲线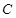 上的动点,点
上的动点,点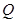 是直线
是直线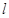 上的动点,求|
上的动点,求| |的最小值.
|的最小值.
本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题记分.
(1)(本小题满分7分)选修4-2:矩阵与变换
若点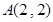 在矩阵
在矩阵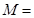
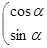
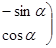 对应变换的作用下得到的点为
对应变换的作用下得到的点为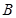
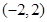 ,求矩阵
,求矩阵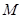 的逆矩阵.
的逆矩阵.
(本小题满分14分)
设直线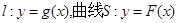 . 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R,都有
. 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R,都有 . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”.
(Ⅰ)已知函数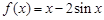 .求证:
.求证: 为曲线
为曲线 的“上夹线”.
的“上夹线”.
(Ⅱ)观察下图:
根据上图,试推测曲线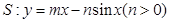 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明.