在平面直角坐标系中,已知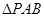 的两个顶点坐标分别是
的两个顶点坐标分别是 、
、 ,另两边
,另两边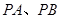 的斜率之积为
的斜率之积为 .
.
(1)求顶点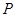 的轨迹
的轨迹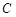 的方程;
的方程;
(2)若轨迹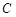 上点
上点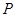 与轨迹
与轨迹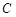 的两焦点构成
的两焦点构成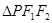 ,且
,且 =
= , 求
, 求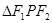 的面积
的面积
已知直线的极坐标方程为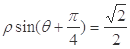 ,圆M的参数方程为
,圆M的参数方程为 。
。
求:(1)将直线的极坐标方程化为直角坐标方程; (2)求圆M上的点到直线的距离的最小值.
某班主任对班级22名学生进行了作业量多少的调查,数据如下表:在喜欢玩电脑游戏的12中,有10人认为作业多,2人认为作业不多;在不喜欢玩电脑游戏的10人中,有3人认为作业多,7人认为作业不多。求:(1)根据以上数据建立一个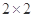 列联表;(2)试问喜欢电脑游戏与认为作业多少是否有关系?
列联表;(2)试问喜欢电脑游戏与认为作业多少是否有关系?
在平面直角坐标系中,以为极点,轴非负半轴为极轴建立坐标系,已知曲线的极坐标方程为,直线的参数方程为: (为参数),两曲线相交于两点. 求:(1)写出曲线的直角坐标方程和直线的普通方程;
(2)若求的值.
已知直线的参数方程为为参数),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,圆的极坐标方程为.求:(1)求圆的直角坐标方程;
(2)若是直线与圆面≤的公共点,求的取值范围.
已知a,b,c为互不相等的非负数,求证:a2+b2+c2>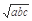 (
(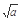 +
+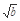 +
+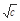 ).
).