下表是某地区的一种传染病与饮用水的调查表:
| |
得病 |
不得病 |
合计 |
| 干净水 |
52 |
466 |
518 |
| 不干净水 |
94 |
218 |
312 |
| 合计 |
146 |
684 |
830 |
利用列联表的独立性检验,判断能否以99.9%的把握认为“该地区的传染病与饮用不干净的水有关”
参考数据：
 |
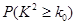0．25 |
0．15 |
0．10 |
0．05 |
0．025 |
0．010 |
0．005 |
0．001 |
 |
1．323 |
2．072 |
2．706 |
3．841 |
5．024 |
6．635 |
7．879 |
10．828 |
已知函数f(x)=x
+4x+3,g(x)为一次函数，若f(g(x))=x+10x+24,求g(x)
的表达式.
已知函数f(x)=
，
(1)求证:函数f(x)在区间(2，+∞）内单调递减；
(2)求函数在x∈[3,5]的最大值和最小值.
已知全集U=R,集合A={x∣x>2或x<-1},集合B={x∣1<x<4},求A∩B,A∪B,(C
A)∩B,(CA)∪(CB)
（本小题12分）离心率为
的椭圆
：
的左、右焦点分别为
、
，
是坐标原点．
（1）求椭圆的方程；
（2）若直线
与交于相异两点
、
，且
，求
．(其中是坐标原点)
（本小题12分）椭圆
的左、右焦点分别为
、
，直线
经过点
与椭圆交于
两点。
（1）求
的周长；
（2）若的倾斜角为
，求的面积。