在一个盒子中，放有标号分别为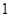
，
，
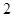的三张卡片，现从这个盒子中，有放回地先后抽得两张卡片的标号分别为
、
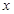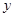，记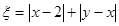
．
（Ⅰ）求随机变量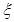
的最大值，并求事件“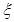取得最大值”的概率；
（Ⅱ）求随机变量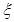的分布列和数学期望．
如图，在△ABC中，∠B＝90°，以AB为直径的圆O交AC于D，过点D作圆O的切线交BC于E，AE交圆O于点F.求证：
(1)E是BC的中点；
(2)AD·AC＝AE·AF.
如图，圆O的直径AB＝2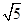
，C是圆O外一点，AC交圆O于点E，BC交圆O于点D，已知AC＝AB，BC＝4，求△ADE的周长．
如图，在△ABC中，已知CM是∠ACB的平分线，△AMC的外接圆交BC于点N.若AC＝
AB，求证：BN＝2AM.
如图，圆O是等腰三角形ABC的外接圆，AB＝AC，延长BC到点D，使CD＝AC，连结AD交圆O于点E，连结BE与AC交于点F.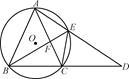
(1)判断BE是否平分∠ABC，并说明理由；
(2)若AE＝6，BE＝8，求EF的长．
如图所示，圆O的两弦AB和CD交于点E，EF∥CB，EF交AD的延长线于点F，FG切圆O于点G.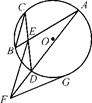
(1)求证：△DEF∽△EFA；
(2)如果FG＝1，求EF的长．