高校招生是根据考生所填报的志愿,从考试成绩所达到的最高第一志愿开始,按顺序分批录取,若前一志愿不能录取,则依次给下一个志愿(同批或下一批)录取.某考生填报了三批共6个不同志愿(每批2个),并对各志愿的单独录取以及能考上各批分数线的概率进行预测,结果如“表一”所示(表中的数据为相应的概率,a、b分别为第一、第二志愿).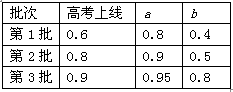
(Ⅰ)求该考生能被第2批b志愿录取的概率;
(Ⅱ)求该考生能被录取的概率;
(Ⅲ)如果已知该考生高考成绩已达到第2批分数线却未能达到第1批分数线,请计算其最有可能在哪个志愿被录取?
(以上结果均保留二个有效数字)
已知盒中装有仅颜色不同的玻璃球6个,其中红球2个、黑球3个、白球1个.
(1)从中任取1个球, 求取得红球或黑球的概率;
(2)列出一次任取2个球的所有基本事件;
(3)从中取2个球,求至少有一个红球的概率.
如图,在直三棱柱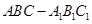 中,
中,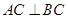 ,点
,点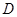 是
是 的中点.
的中点.
求证:(1) ;(2)
;(2) 平面
平面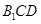 .
.
已知角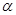 的终边在
的终边在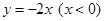 上,求
上,求
(1)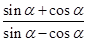 的值;
的值;
(2) 的值.
的值.
已知函数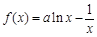 ,
,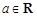 .
.
(1)若曲线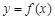 在点
在点 处的切线与直线
处的切线与直线 垂直,求
垂直,求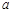 的值;
的值;
(2)求函数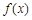 的单调区间;(3)当
的单调区间;(3)当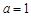 ,且
,且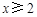 时,证明:
时,证明: .
.
已知抛物线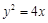 ,点
,点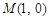 关于
关于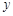 轴的对称点为
轴的对称点为 ,直线
,直线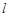 过点
过点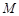 交抛物线于
交抛物线于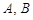 两点.
两点.
(1)证明:直线 的斜率互为相反数;
的斜率互为相反数;
(2)求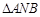 面积的最小值;
面积的最小值;
(3)当点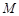 的坐标为
的坐标为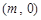 ,
, 且
且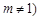 .根据(1)(2)推测并回答下列问题(不必说明理由):
.根据(1)(2)推测并回答下列问题(不必说明理由):
①直线 的斜率是否互为相反数? ②
的斜率是否互为相反数? ②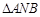 面积的最小值是多少?
面积的最小值是多少?