姚明是我国著名的篮球运动员，他在2005

姚明是我国著名的篮球运动员，他在2005－2006赛季NBA常规赛中表现非常优异。下面是他在这个赛季中，分期与“超音速队”和“快船队”各四场比赛中的技术统计。

场次	对阵超音速	对阵快船
得分	篮板	失误	得分	篮板	失误
第一场	22	10	2	25	17	2
第二场	29	10	2	29	15	0
第三场	24	14	2	17	12	4
第四场	26	10	5	22	7	2

（1）请分别计算姚明在对阵“超音速”和“快船”两队的各四场比赛中，平均每场得多少分？
（2）请你从得分的角度分析，姚明在与“超音速”和“快船”的比赛中，对阵哪一个队的发挥更稳定？
（3）如果规定“综合得分”为：平均每场得分×1＋平均每场篮板×1．5十平均每场失误×（－1.5），且综合得分越高表现越好，那么请你利用这种评价方法，来比较姚明在分别与“超音速”和“快船”的各四场比赛中，对阵哪一个队表现更好？

科目数学题型解答题难度中等

知识点：统计量的选择

已知：四边形 $OABC$ 是菱形，以 $O$ 为圆心作 $⊙ O$ ，与 $BC$ 相切于点 $D$ ，交 $OA$ 于 $E$ ，交 $OC$ 于 $F$ ，连接 $OD$ ， $DF$ ．

（1）求证： $AB$ 是 $⊙ O$ 的切线；

（2）连接 $EF$ 交 $OD$ 于点 $G$ ，若 $∠ C = 45 °$ ，求证： $G F^{2} = DG \cdot OE$ ．

超速行驶是一种十分危险的违法驾驶行为，在一条笔直的高速公路 $MN$ 上，小型车限速为每小时120千米，设置在公路旁的超速监测点 $C$ ，现测得一辆小型车在监测点 $C$ 的南偏西 $30 °$ 方向的 $A$ 处，7秒后，测得其在监测点 $C$ 的南偏东 $45 °$ 方向的 $B$ 处，已知 $BC = 200$ 米， $B$ 在 $A$ 的北偏东 $75 °$ 方向，请问：这辆车超速了吗？通过计算说明理由．（参考数据： $\sqrt{2} \approx 1.41$ ， $\sqrt{3} \approx 1.73)$

某电子超市销售甲、乙两种型号的蓝牙音箱，每台进价分别为240元，140元，下表是近两周的销售情况：

销售时段	销售数量		销售收入
销售时段	甲种型号	乙种型号	销售收入
第一周	3台	7台	2160元
第二周	5台	14台	4020元

（1）求甲、乙两种型号蓝牙音箱的销售单价；

（2）若超市准备用不多于6000元的资金再采购这两种型号的蓝牙音箱共30台，求甲种型号的蓝牙音箱最多能采购多少台．

传统节日“端午节”的早晨，小文妈妈为小文准备了四个粽子作早点：一个枣馅粽，一个肉馅粽，两个花生馅粽，四个粽子除内部馅料不同外，其它一切均相同．

（1）小文吃前两个粽子刚好都是花生馅粽的概率为　 $\frac{1}{6}$ 　；

（2）若妈妈在早点中给小文再增加一个花生馅的粽子，则小文吃前两个粽子都是花生馅粽的可能性是否会增大？请说明理由．

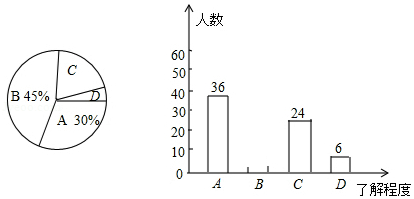
今年市委市政府积极推进创建"全国文明城市"工作，市创城办公室为了调查初中学生对"社会主义核心价值观"内容的了解程度（程度分为：" $A -$ 十分熟悉"，" $B -$ 了解较多"，" $C -$ 了解较少"，" $D -$ 不知道" $)$ ，对我市一所中学的学生进行了随机抽样调查，根据调查结果绘制了两幅不完整的统计图如图，根据信息解答下列问题：

（1）本次抽样调查了多少名学生；

（2）补全条形统计图和扇形统计图；

（3）求扇形统计图中" $D -$ 不知道"所在的扇形圆心角的度数；

（4）若该中学共有2400名学生，请你估计这所中学的所有学生中，对"社会主义核心价值观"内容的了解程度为"十分熟悉"和"了解较多"的学生共有多少名？