如图,抛物线F: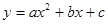 的顶点为P,抛物线:与y轴交于点A,与直线OP交于点B.过点P作PD⊥x轴于点D,平移抛物线F使其经过点A、D得到抛物线F′:
的顶点为P,抛物线:与y轴交于点A,与直线OP交于点B.过点P作PD⊥x轴于点D,平移抛物线F使其经过点A、D得到抛物线F′: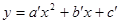 ,抛物线F′与x轴的另一个交点为C.
,抛物线F′与x轴的另一个交点为C.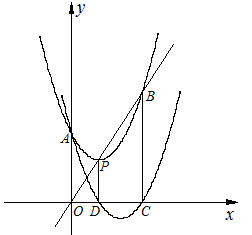
⑴当a = 1,b=-2,c = 3时,求点C的坐标(直接写出答案);
⑵若a、b、c满足了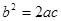
①求b:b′的值;
②探究四边形OABC的形状,并说明理由.
某校九年级一班数学调研考试成绩绘制成频数分布直方图,如图(得分取整数).
请根据所给信息解答下列问题:
这个班有多少人参加了本次数学调研考试?
 ~
~ 分数段的频数和频率各是多少?
分数段的频数和频率各是多少?请你根据统计图,提出一个与(1),(2)不同的问题,并给出解答.
如图1,在直角坐标系xoy中,O是坐标原点,点A在x正半轴上,OA=12cm,点B在y轴的正半轴上,OB=12cm,动点P从点O开始沿OA以2cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t(0<t<6)s.求∠OA
 B的度数
B的度数以OB为直径的⊙O′与AB交于点M,当t为何值时,PM与⊙O′相切?
是否存在△RPQ为等腰三角形?若存在,请直接写出t值;若不存在,请说明理由.

某地为促进特种水产养殖业的发展,决定对甲鱼和黄鳝的 养殖提供政府补贴.该地某农户在改建的10个1亩大小的水池里分别养殖甲鱼和黄鳝,因资金有限,投入不能超过14万元,并希望获得不低于10.8万元的收益,相关信息如下表所示:
养殖提供政府补贴.该地某农户在改建的10个1亩大小的水池里分别养殖甲鱼和黄鳝,因资金有限,投入不能超过14万元,并希望获得不低于10.8万元的收益,相关信息如下表所示:
| 养殖种类 |
成本 (万元/亩) |
毛利润 (万元/亩) |
政府补贴 (万元/亩) |
| 甲鱼 |
1.5 |
2.5 |
0.2 |
| 黄鳝 |
1 |
1.8 |
0.1 |
根据以上信息,该农户可以怎样安
 排养殖
排养殖应怎样安排养殖,可获得最大收益?(收益=毛利润-成本+政府补贴)
据市场调查,在养殖成本不变的情况下,黄鳝的毛利润相对稳定,而每亩甲鱼的毛利润将减少m万元.问该农户又该如何安排养殖,才可获得最大收益?
请阅读材料并填空:
问题:如图1,在等边三角形ABC内有一点P,且PA=2,PB=,PC=1.求∠BPC的度数和等边三角形ABC的边长.
李明同学的思路是:将△BPC绕点B顺时针旋转60°,画出旋转后的图形(如图2).连结PP′.
根据李明同学的思路,进一步思考后可求得∠BPC=____°,等边△ABC的边长为____.请你参考李明同学的思路,探究并解决下列问题:如图3,在正方形ABCD内有一点P,且PA=,BP=,PC=1.求∠BPC的度数和正方形ABCD的边长.

安装在屋顶的太阳能热水器的横截面示意图如图所示.已知安装集热管的支架AE与支架BF所在直线相交于水箱横截面⊙O的圆心O,支架BF的长度为0.9m,且与屋面AB垂直,支架AE的长度为1.7m,且与铅垂线OD的夹角为35°,支架的支撑点A、B在屋面上的距离为1.6m.
求⊙O的半径;
求屋面AB与水平线AD的夹角(精确到1°)