如图,BD、CE是△ABC的两条高,它们交于O点。
⑴∠1和∠2的大小关系如何?并说明理由;
 ⑵若∠A=500,∠ABC=700,求∠3和∠4的度数。
⑵若∠A=500,∠ABC=700,求∠3和∠4的度数。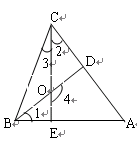
尺规作图题(不写作图步骤,保留作图痕迹).
已知:如图,求作线段AB的垂直平分线.
如图,在△ABC中,AB=AC,D是BA延长线上一点,点E是AC的中点.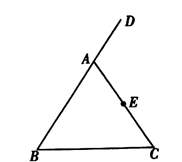
(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(不写作法,但必须保留作图痕迹)
①作∠DAC的平分线AM,
②连接BE并延长交AM与点F
(2)猜想与证明:试猜想AF与BC有怎样的位置关系和数量关系,并说明理由.
已知:如图,在△ABC中,AB=AC,点D在AB上,且CB=CD=AD
求:△CBD各角的度数
如图,E、F分别是等边三角形ABC的边AB、AC上的点,且BE=AF,CE、BF交于点P.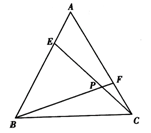
(1)求证:CE=BF;
(2)求∠BPC的度数.
如图1所示,等边△ABC中,AD是BC边上的中线,根据等腰三角形的“三线合一”特性,AD平分∠BAC,且AD⊥BC,则有∠BAD=30°,BD=CD=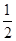 AB.于是可得出结论“直角三角形中,30°角所对的直角边等于斜边的一半”.
AB.于是可得出结论“直角三角形中,30°角所对的直角边等于斜边的一半”.
请根据从上面材料中所得到的信息解答下列问题:
(1)△ABC中,若∠A:∠B:∠C=1:2:3,AB=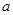 ,则BC= ;
,则BC= ;
(2)如图2所示,在△ABC中,∠ACB=90°,BC的垂直平分线交AB于点D,垂足为E,当BD=5cm,∠B=30°时,△ACD的周长= .
(3)如图3所示,在△ABC中,AB=AC,∠A=120°,D是BC的中点,DE⊥AB,垂足为E,那么BE:EA= .
(4)如图4所示,在等边△ABC中,D、E分别是BC、AC上的点,且∠CAD=∠ABE,AD、BE交于点P,作BQ⊥AD于Q,猜想PB与PQ的数量关系,并说明理由.