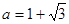如下图，直角梯形ABCD中，AD∥BC，AD=24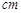
，BC=26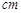，∠B=90°，动点P从A开始沿AD边向D以1
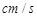的速度运动，动点Q从点C开始沿CB以3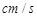的速度向点B运动．P、Q同时出发，当其中一点到达顶点时，另一点也随之停止运动，设运动时间为
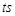，问
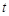为何值时，（1）四边形PQCD是平行四边形．（2）当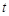为何值时，四边形PQCD为等腰梯形．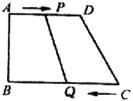
请判断关于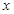
的一元二次方程
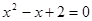的根的情况，并说明理由．如果方程有根，请写出方程的根；如果没有根，请通过只改变常数项的值，写出一个有实数根的一元二次方程．
在一个口袋中有3个完全相同的小球，把它们分别标号为1、2、3，随机地摸取一个小球后放回，再随机地摸出一个小球，求“两次取的小球的标号相同”的概率，请借助列表法或树形图说明理由．
（本题12分）如图，两个同样大小的等边△ABC和△ACD，边长为a，它们拼成一个菱形ABCD，另一个足够大的等边△AEF绕点A旋转，AE与BC相交于点M，AF与CD相交于点N。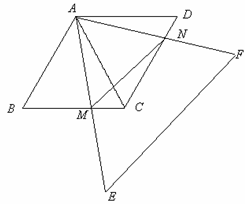
（1）证明：∠DAN=∠CAM;
（2）求四边形AMCN的面积；
（3）探索△AMN何时面积最小，并写出这个最小面积的值.
（本题5分）如图，已知⊙O的半径为5cm，弦AB的长是8cm。求圆心O到弦AB的距离。
（本题5分）先化简，再求值：
，其中 