在正方形ABCD中，对角线AC，BD交于点O，点P在线段BC上（不含点B），∠BPE＝
∠ACB，PE交BO于点E，过点B作BF⊥PE，垂足为F，交AC于点G．
（1） 当点P与点C重合时（如图①）．求证：△BOG≌△POE；
（2）通过观察、测量、猜想：
= ，并结合图②证明你的猜想；
（3）把正方形ABCD改为菱形，其他条件不变（如图③），若∠ACB=α，求的值．（用含α的式子表示）
我国年人均用纸量约为28公斤，每个初中毕业生离校时大约有10公斤废纸；用1吨废纸造出的再生好纸，所能节约的造纸木材相当于18棵大树，而平均每亩森林只有50至80棵这样的大树．（1）若我市2011年5万名初中毕业生能把自己离校时的全部废纸送到回收站使之制造为再生好纸，那么最少可使多少亩森林免遭砍伐？
（2）我市从2000年初开始实施天然林保护工程，大力倡导废纸回收再生，如今成效显著，森林面积大约由2009年初的1500万亩增加到2011年初的1815万亩．假设我市年用纸量的20%可以作为废纸回收、森林面积年均增长率保持不变，请你按全市总人口约为400万计算：在从2011年初到2012年初这一年度内，我市新增加的森林面积与因回收废纸所能保护的森林面积之和最多可能达到多少亩.
如图，已知在直角梯形ABCD中，AD∥BC，AB⊥BC，AD=11，BC=13，
AB=12．动点P、Q分别在边AD和BC上，且BQ=3DP．线段PQ与BD相交于点E，过点E作EF∥BC，交CD于点F，射线PF交BC的延长线于点G，设DP=x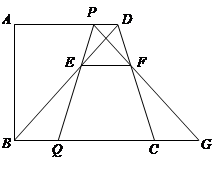
（1）求
的值．（2）当点P运动时，试探究四边形EFGQ的面积是否会发生变化？如果发生变化，请用x的代数式表示四边形EFGQ的面积S；如果不发生变化，请求出这个四边形的面积S．
两个完全相同的矩形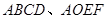
按如图所示的方式摆放，使点
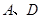均在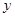
轴的正半轴上，点B在第一象限，点
在
轴的正半轴上，点
在函数
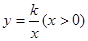的图象上
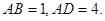
(1)求
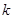的值．(2)将矩形
绕点B顺时针旋转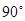
得到矩形
边
交函数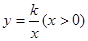的图象于点
求
的长．
已知：如图，梯形
中，
平分
分别为AD、AB中点，点G为BC边上一点，且
(1)求证：
；(2)猜想：当
时，四边形
为平行
四边形，并说明理由.
江西庐山是驰名中外的名山，为提高游客到庐山某景点的安全性，决定将到达该景点的步行台阶进行改造，把倾角由45°减至30°，已知原台
阶坡面AB的长为
m（BC所在地面为水平面）．
（1）改造后的台阶坡面会加长多少？
（2）改造后的台阶比原来的台阶多占多长一段水平地面？