(本小题满分10分)某班主任对班级22名学生进行了作业量多少的调查,数据如下表:在喜欢玩电脑游戏的12中,有10人认为作业多,2人认为作业不多;在不喜欢玩电脑游戏的10人中,有3人认为作业多,7人认为作业不多.
(1)根据以上数据建立一个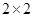 列联表;
列联表;
(2)试问喜欢电脑游戏与认为作业多少是否有关系?
某通讯公司需要在三角形地带 区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域
区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域 内,乙中转站建在区域
内,乙中转站建在区域 内.分界线
内.分界线 固定,且
固定,且 =
= 百米,边界线
百米,边界线 始终过点
始终过点 ,边界线
,边界线 满足
满足 .
.
设 (
( )百米,
)百米, 百米.
百米.
(1)试将 表示成
表示成 的函数,并求出函数
的函数,并求出函数 的解析式;
的解析式;
(2)当 取何值时?整个中转站的占地面积
取何值时?整个中转站的占地面积 最小,并求出其面积的最小值.
最小,并求出其面积的最小值.
已知复数 .
.
(1)求 的最小值;
的最小值;
(2)设 ,记
,记 表示复数z的虚部).将函数
表示复数z的虚部).将函数 的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把所得的图像向右平移
的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把所得的图像向右平移 个单位长度,得到函数
个单位长度,得到函数 的图像.试求函数
的图像.试求函数 的解析式.
的解析式.
已知矩形 是圆柱体的轴截面,
是圆柱体的轴截面, 分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为
分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为 ,且该圆柱体的体积为
,且该圆柱体的体积为 ,如图所示.
,如图所示.
(1)求圆柱体的侧面积 的值;
的值;
(2)若 是半圆弧
是半圆弧 的中点,点
的中点,点 在半径
在半径 上,且
上,且 ,异面直线
,异面直线 与
与 所成的角为
所成的角为 ,求
,求 的值.
的值.
已知函数 是定义域为
是定义域为 的偶函数.当
的偶函数.当 时,
时, 若关于
若关于 的方程
的方程
 有且只有7个不同实数根,则
有且只有7个不同实数根,则 的值是.
的值是.
(理)已知点 是平面直角坐标系上的一个动点,点
是平面直角坐标系上的一个动点,点 到直线
到直线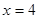 的距离等于点
的距离等于点 到点
到点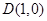 的距离的2倍.记动点
的距离的2倍.记动点 的轨迹为曲线
的轨迹为曲线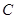 .
.
(1)求曲线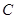 的方程;
的方程;
(2)斜率为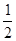 的直线
的直线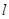 与曲线
与曲线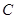 交于
交于 两个不同点,若直线
两个不同点,若直线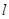 不过点
不过点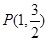 ,设直线
,设直线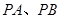 的斜率分别为
的斜率分别为 ,求
,求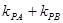 的数值;
的数值;
(3)试问:是否存在一个定圆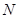 ,与以动点
,与以动点 为圆心,以
为圆心,以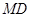 为半径的圆相内切?若存在,求出这个定圆的方程;若不存在,说明理由.
为半径的圆相内切?若存在,求出这个定圆的方程;若不存在,说明理由.