学校开展综合实践活动中，某班进行了小制作评比，作品上交时间为5月11日至5月30日，评委们把同学们上交作品的件数按5天一组分组统计，绘制了频数分布直方图如下，小长方形的高之比为：2：5：2：1．现已知第二组的上交作品件数是20件．求：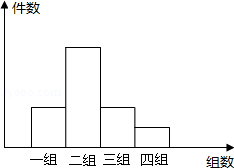
（1）此班这次上交作品共 件；
（2）评委们一致认为第四组的作品质量都比较高，现从中随机抽取2件作品参加学校评比，小明的两件作品都在第四组中，他的两件作品都被抽中的概率是多少？（请写出解答过程）
已知如图AB∥CD，∠ABE=3∠ABF, ∠CDE=3∠CDF,试求∠E与∠F的比。
如图B点在A处的南偏西45°方向，C处在A处的南偏东15°方向，C处在B北偏东80°方向，求∠ACB。
如图，直线AB∥CD，直线AB、CD被直线EF所截，EG平分∠BEF，FG平分∠DFE，请问∠G等于多少度？写出完整的说理过程．
阅读：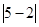 
表示5与2差的绝对值，也可理解为5与2两数在数轴上所
对应的两点之间的距离；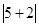
可以看做
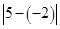，表示5与－2的差的绝对值，也
可理解为5与－2两数在数轴上所对应的两点之间的距离．
探索: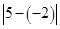=___________利用数轴，找出所有符合条件的整数
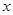，使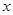所表示的点到5和—2的距离之和为7由以上探索猜想，对于任何有理数
，
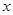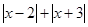是否有最小值? 如果有，写出最
小值；如果没有，说明理由
某单位在五月份准备组织部分员工到北京旅游，现联系了甲、乙两家旅行社，两家旅行社报价均为2000元/人，两家旅行社同时都对10人以上的团体推出了优惠举措：甲旅行社对每位员工七五折优惠；而乙旅行社是免去一位带队管理员工的费用，其余员工八折优惠.如果设参加旅游的员工共有a（a
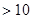）人，则甲旅行社的费用为元，乙旅行社的费用为元；（用含a的代数式表示，并化简.）假如这个单位现组织包括管理员工在内的共20名员工到北京旅游，该单位选择哪一家旅行社比较优惠？请说明理由.
如果计划在五月份外出旅游连续七天，设最中间一天的日期为
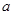，则这七天的日期之和为.（用含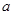的代数式表示，并化简.）假如这七天的日期之和为63的倍数，则他们可能于五月几号出发?（写出所有符合条件的可能性，并写出简单的计算过程.）