如图,直线AB∥CD,直线AB、CD被直线EF所截,EG平分∠BEF,FG平分∠DFE,请问∠G等于多少度?写出完整的说理过程.
(本小题满分6分)
在如图所示的方格纸中,△ABC的顶点都在小正方形的顶点上,以小正方形互相垂直的两边所在直线建立直角坐标系.
(1)作出△ABC关于y轴对称的△A1B1C1,其中A,B,C分别和A1,B1,C1对应;
(2)平移△ABC,使得A点在x轴上,B点在y轴上,平移后的三角形记为△A2B2C2,作出平移后的△A2B2C2,其中A,B,C分别和A2,B2,C2对应;
(3)填空:在(2)中,设原△ABC的外心为M,△A2B2C2的外心为M,则M与M2之间的距离为.
推理证明(本小题满分6分)
如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D,AB=AD.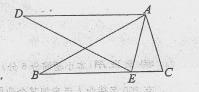
(1)求证:△ABC≌△ADE;
(2)如果∠AEC=75°,将△ADE绕着点A旋转一个锐角后与△ABC重合,求旋转角的大小.
运算求解(本小题满分10分)
解方程或不等式组;
(1)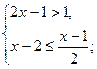
(2)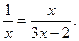
计算化简(本小题满分10分)
(1)
(2)
(本小题满分12分)
已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB = ∠EDF = 90°,∠DEF = 45°,AC =" 8" cm,BC =" 6" cm,EF =" 9" cm.
如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动.DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).
解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由.
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.