南中国海是中国固有领海，我渔政船经常在此海域执勤巡察．一天我渔政船停在小岛A北偏西37°方向的B处，观察A岛周边海域．据测算,渔政船距A岛的距离AB长为10海里．此时位于A岛正西方向C处的我渔船遭到某国军舰的袭扰，船长发现在其北偏东50°的方向上有我方渔政船，便发出紧急求救信号．渔政船接警后，立即沿BC航线以每小时30海里的速度前往救助，问渔政船大约需多少分钟能到达渔船所在的C处？
(参考数据：sin37°≈0.60，cos37°≈0.80，sin50°≈0.77，cos50°≈0.64，sin53°≈0.80，cos53°≈0.60，sin40°≈0.64，cos40°≈0.77)
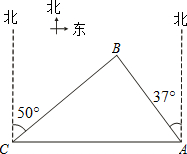
先化简，再求值: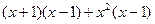
，其中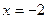
.
如图，边长为4的正方形OABC的顶点O为坐标原点，点A
在x轴的正半轴上，点C在y轴的正半轴上．动点D在线段BC上移动（不与B，C重合），
连接OD，过点D作DE⊥OD，交边AB于点E，连接OE。
（1）当CD=1时，求点E的坐标；
（2）如果设CD=t，梯形COEB的面积为S，那么是否存在S的最大值？若存在，请求出这
个最大值及此时t的值；若不存在，请说明理由。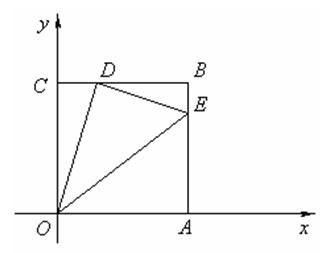
如图所示，△ABC内接于⊙O，AB是⊙O的直径，点D在⊙O
上，过点C的切线交AD的延长线于点E，且AE⊥CE，连接CD．
（1）求证：DC=BC；
（2）若AB=5，AC=4，求tan∠DCE的值．
如图，在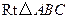
中，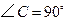
，
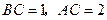，把边长分别为
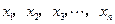的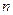
个正方形依次放入
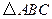中，请回答下列问题：
（1）按要求填表
（2）第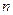个正方形的边长
；
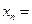（3）若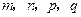
是正整数，且
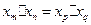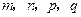，试判断的关系．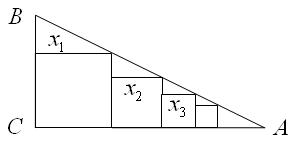
将一条长为20cm的铁丝剪成两段，并以每一段铁丝的长度为周长做成一个正方形．
（1）要使这两个正方形的面积之和等于
，那么这段铁丝剪成两段后的长度分别是多少？
（2）两个正方形的面积之和可能等于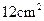
吗？若能，求出两段铁丝的长度；若不能，请说明理由．