如图1，已知正方形ABCD，将一个45度角
的顶点放在D点并绕D点旋转，角的两边分别交AB边和BC边于点E和F，连接EF。求证：EF＝AE+CF
（1） 小明是这样思考的:延长BC到G，使得CG＝AE，连接DG，先证△DAE≌△DCG，再证△DEF≌△DGF，请你借助图2，按照小明的思路，写出完整的证明思路。
（2）刘老师看到这条题目后，问了小明两个小问题：①如果正方形的边长和△BEF的面积都等于6，求EF的长；②将角绕D点继续旋转，使得角的两边分别和AB边延长线、BC边的延长线交于E和F，如图3所示，猜想EF、AE、CF三线段之间的数量关系并给予证明。请你帮忙解决。
如图，点P在平行四边形ABCD的CD边上，连接BP并延长与AD的延长线交于点Q．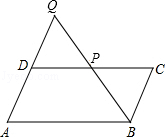
（1）求证：△DQP∽△CBP；
（2）当△DQP≌△CBP，且AB=8时，求DP的长．
本题为选项做题，从甲、乙两题中选做一题即可，如果两题都做，只以甲题计分．
甲：直线l：y=（m﹣3）x+n﹣2（m，n为常数）的图象如图1所示，化简：|m﹣n|﹣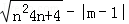
；
乙：已知：如图2，在边长为a的正方形ABCD中，M是边AD的中点，能否在边AB上找到点N（不含A、B），使得△MAN相似？若能，请给出证明；若不能，请说明理由．
在△ABC中，AB=18cm，AC=15cm，点D是AB边上一点，且AD=6cm，点E是AC上一点，当AE为何值时，△ABC与△ADE相似？
已知：如图，在Rt△ABC中，∠ACB=90°，CD是AB上的中点，过点B作BE⊥CD，垂足为E．
求证：△ABC∽△BCE．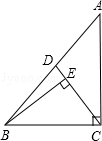
如图，在矩形ABCD中，E是AD边上点，∠CEF=90°，EF交AB边于F，
（1）若矩形ABCD的周长为10，设AB=x（0＜x≤4），BC=y．写出y与x的函数关系式，并在直角坐标系中画出此函数图象；
（2）求证：△AFE∽△DEC．