某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时,有如下探讨:
甲同学:我发现这种多边形不一定是正多边形.如圆内接矩形不一定是正方形.
乙同学:我知道边数为3时,它是正三角形;我想,边数为5时,它可能也是正五边形…
丙同学:我发现边数为6时,它也不一定是正六边形.如图2,△ABC是正三角形,弧AD、弧BE、弧CF均相等,这样构造的六边形ADBECF不是正六边形.
(1)如图1,若圆内接五边形ABCDE的各内角均相等,则∠ABC= °,并简要说明圆内接五边形ABCDE为正五边形的理由;
(2)如图2,请证明丙同学构造的六边形各内角相等;
(3)根据以上探索过程,就问题“各内角都相等的圆内接多边形是否为正多边形”的结论与“边数n(n≥3,n为整数)”的关系,提出你的猜想(不需证明).
如图,已知⊙O的弦CD垂直于直径AB,点E在CD上,且EC=EB.
(1)求证:△CEB∽△CBD;
(2)若CE=3,CB=5,求DE的长.
抛物线y=﹣x2+(m﹣1)x+m与y轴交于点(0,3).
(1)求抛物线的解析式;
(2)求抛物线与坐标轴的交点坐标;
(3)①当x取什么值时,y>0?②当x取什么值时,y的值随x的增大而减小?
已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.
在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共5只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
| 摸球的次数n |
100 |
150 |
200 |
500 |
800 |
1000 |
| 摸到白球的次数m |
58 |
96 |
116 |
295 |
484 |
601 |
摸到白球的频率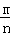 |
0.58 |
0.64 |
0.58 |
0.59 |
0.605 |
0.601 |
(1)请估计:当n很大时,摸到白球的频率将会接近 ;(精确到0.1)
(2)试估算口袋中白种颜色的球有多少只?
(3)请画树状图或列表计算:从中先摸出一球,不放回,再摸出一球;这两只球颜色不同的概率是多少?