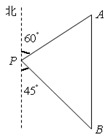
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标我(4,-1).
(1)把△ABC向上平移5个单位后得到对应的△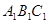 ,画出△
,画出△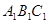 的图形并写出点
的图形并写出点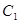 的坐标;
的坐标;
(2)以原点O为对称中心,再画出与△ 关于原点对称的△
关于原点对称的△ ,并写出点
,并写出点 的坐标.
的坐标.
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+3的顶点为M(2,-1),交x轴于A、B两点,交y轴于点C,其中点B的坐标为(3,0).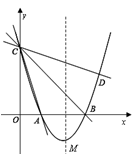
(1)求该抛物线的解析式;
(2)设经过点C的直线与该抛物线的另一个交点为D,且直线CD和直线CA关于直线BC对称,求直线CD的解析式;
(3)在该抛物线的对称轴上存在点P,满足PM2+PB2+PC2=35,求点P的坐标.
操作与实践: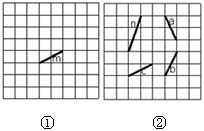
(1)在图①中,以线段m为一边画菱形,要求菱形的顶点均在格点上.(画出所有符合条件的菱形)
(2)在图②中,平移a、b、c中的两条线段,使它们与线段n构成以n为一边的等腰直角三角形.(画一个即可)
小赵投资销售一种进价为每件20元的护眼台灯.销售过程中发现,月内销售单价不变,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数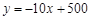 .
.
(1)设小赵每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?并求出最大利润.
(2)如果小赵想要每月获得的利润不低于2000元,那么如何制定销售单价才可以实现这一目标?
如图①,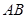 为⊙
为⊙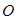 的直径,
的直径,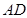 与⊙
与⊙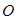 相切于点
相切于点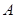 ,
, 与⊙
与⊙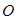 相切于点
相切于点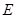 ,点
,点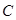 为
为 延长线上一点,且CE=CB.
延长线上一点,且CE=CB.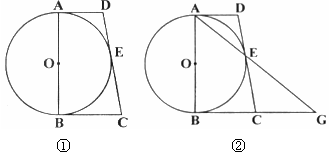
(1)求证: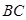 为⊙
为⊙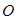 的切线;
的切线;
(2)如图②,连接AE,AE的延长线与BC的延长线交于点G.若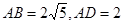 ,求线段BC和EG的长.
,求线段BC和EG的长.
某学生参加社会实践活动,在景点P处测得景点B位于南偏东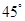 方向,然后沿北偏东
方向,然后沿北偏东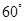 方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之的距离.
方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之的距离.