已知偶函数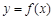 满足:当
满足:当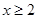 时,
时, ,
,
当 时,
时,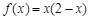
(1) 求当 时,
时,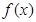 的表达式;
的表达式;
(2) 试讨论:当实数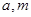 满足什么条件时,函数
满足什么条件时,函数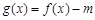 有4个零点,
有4个零点,
且这4个零点从小到大依次构成等差数列.
(本小题满分12分)
某商场准备在国庆节期间举行促销活动,根据市场调查,该商场决定从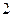 种服装商品,
种服装商品, 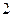 种家电商品,
种家电商品, 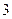 种日用商品中,选出
种日用商品中,选出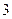 种商品进行促销活动.
种商品进行促销活动.
(Ⅰ)试求选出的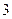 种商品中至多有一种是家电商品的概率;
种商品中至多有一种是家电商品的概率;
(Ⅱ)商场对选出的某商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高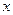 元,同时,若顾客购买该商品,则允许有
元,同时,若顾客购买该商品,则允许有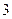 次抽奖的机会,若中奖,则每次中奖都获得数额为
次抽奖的机会,若中奖,则每次中奖都获得数额为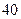 元的奖券.假设顾客每次抽奖时获奖的概率都是
元的奖券.假设顾客每次抽奖时获奖的概率都是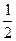 ,若使促销方案对商场有利,则
,若使促销方案对商场有利,则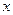 最少为多少元?
最少为多少元?
(本小题满分12分)
如图,在直三棱柱ABC—A1B1C1中,AC=1,AB= ,BC=
,BC= ,AA1=
,AA1= 。
。
(I)求证:A1B⊥B1C;
(II)求二面角A1—B1C—B的大小。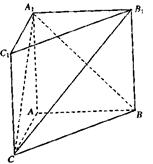
(本小题满分12分)
若不等式 对一切正整数n都成立,求正整数a的最大值,并用数学归纳法证明你的结论。
对一切正整数n都成立,求正整数a的最大值,并用数学归纳法证明你的结论。
(本小题满分10分)
已知函数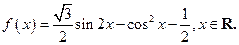
(I)求函数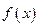 的最小值和最小正周期;
的最小值和最小正周期;
(II)设 的内角
的内角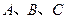 的对边分别为
的对边分别为 ,且
,且 ,若向量
,若向量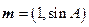 与向量
与向量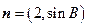 共线,求
共线,求 的值.
的值.
2条直线将一个平面最多分成4部分,3条直线将一个平面最多分成7部分, 4条直线将一个平面最多分成11部分,……; ,
, ,
, ;……
;……
(1) 条直线将一个平面最多分成多少个部分(
条直线将一个平面最多分成多少个部分( >1)?证明你的结论;
>1)?证明你的结论;
(2) 个平面最多将空间分割成多少个部分(
个平面最多将空间分割成多少个部分( >2)?证明你的结论
>2)?证明你的结论