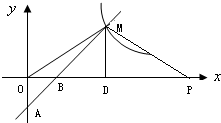
如图,上面是一些具体的物体,下面是一些立体图形, 试找出与下面立体图形相类似的实物 (用线连接).
如图,某电视台大楼顶部安置了一电视发射铁塔CD,现有一位测试员分别在楼下相距16m的A,B两处测得D点和C点的仰角分别是45°和60°,已知A,B,E在一条直线上,C,D,E也在一条直线上,且BE=30m.求电视发射铁塔的高度.(结果保留整数,参考数据:≈1.41,≈1.73)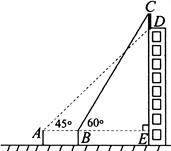
如图,抛物线y=a(x+1)(x-5)与x轴的交点为M、N.直线y=kx+b
与x轴交于P(-2,0),与y轴交于C.若A、B两点在直线y=kx+b上,且AO=BO=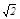 ,AO⊥BO.D为线段MN的中点,OH为Rt△OPC斜边上的高.
,AO⊥BO.D为线段MN的中点,OH为Rt△OPC斜边上的高.OH的长度等于___________;k=___________,b=____________;
是否存在实数a,使得抛物线y=a(x+1)(x-5)上有一点E,满足以D、N、E为顶点的三角形与△AOB相似?若不存在,说明理由;若存在,求所有符合条件的抛物线的解析式,同时探索所求得的抛物线上是否还有符合条件的E点(简要说明理由);并进一步探索对符合条件的每一个E点,直线NE与直线AB的交点G是否总满足PB·PG<
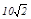 ,写出探索过程.
,写出探索过程.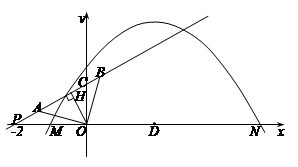
小王家是新农村建设中涌现出的 “养殖专业户”.他准备购置80只相同规格的网箱,养殖A、B两种淡水鱼(两种鱼不能混养).计划用于养鱼的总投资不少于7万元,但不超过7.2万元,其中购置网箱等基础建设需要1.2万元.设他用x只网箱养殖A种淡水鱼,目前平均每只网箱养殖A、B两种淡水鱼所需投入及产业情况如下表:
项目类别 |
鱼苗投资 (百元) |
饲料支出 (百元) |
收获成品鱼(千克) |
成品鱼价格 (百元/千克) |
| A种鱼 |
2.3 |
3 |
100 |
0.1 |
| B种鱼 |
4 |
5.5 |
55 |
0.4 |
小王有哪几种养殖方式?
哪种养殖方案获得的利润最大?
根据市场调查分析,当他的鱼上市时,两种鱼的价格会有所变化,A种鱼价格上涨a%(0<a<50),B种鱼价格下降20%,考虑市场变化,哪种方案获得的利润最大?(利润=收入-支出.收入指成品鱼收益,支出包括基础建设投入、鱼苗投资及饲料支出)
如图,已知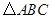 ,以
,以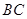 为直径,
为直径,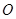 为圆心的半圆交
为圆心的半圆交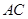 于点
于点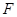 ,点
,点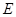 为弧CF的中点,连接
为弧CF的中点,连接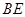 交
交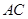 于点
于点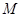 ,
,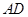 为△ABC的角平分线,且
为△ABC的角平分线,且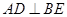 ,垂足为点
,垂足为点 .
.求证:
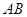 是半圆
是半圆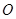 的切线;
的切线;若
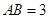 ,
,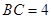 ,求
,求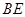 的长.
的长.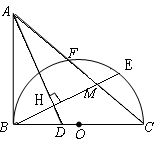
如图,一次函数y=k1x+b的图象经过A(0,-2),B(1,0)两点,与反比例函数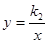 的图象在第一象限内的交点为M,若△OBM的面积为2.
的图象在第一象限内的交点为M,若△OBM的面积为2.求一次函数和反比例函数的表达式;
在x轴上是否存在点P,使AM⊥MP?若存在,求出点P的坐标;若不存在,说明理由.