公路上同向而行的两辆汽车,从后车车头与前车车尾“相遇”到原后车车尾离开原车车头这段时间为超车时间,如果原前、后两车车长分别为a、b,那么在超车时间内两车行驶的路程与两车车长有何关系?
如图,已知△ABC为等腰直角三角形,点D为边BC上的一动点(点D不与B、C重合),以AD为边作正方形ADEF(A、D、E、F按逆时针排列),连接CF。求证: CF+CD=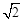 AC。
AC。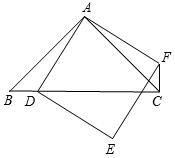
已知,如图,AB是⊙O的直径,弦CD⊥AB于点E,CD=6,AE=4,点P为弧CBD上的动点(P不与C、D重合),连结AP交CD于点F,证明:AF·AP=25。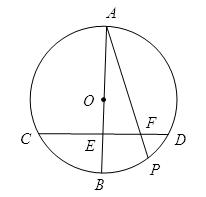
如图,已知半圆O的直径AB,将—个三角板的直角顶点固定在圆心O上,当三角板绕着点O转动时,三角板的两条直角边与半圆圆周分别交于C、D两点,连结AD、BC交于点E.线段BD是否恒等于DE,若是请证明,若不是请说明理由.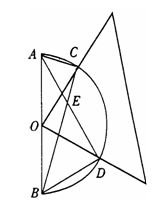
已知抛物线C1的解析式为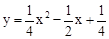 .将抛物线C1向下平移h个单位(h>0)得到抛物线C2.一条平行于x轴的直线与两条抛物线交于A、B、C、D四点(如图),且点A、C关于y轴对称,直线AB与x轴的距离是m2(m>0)。若抛物线C1的对称轴与直线AB交于点E,与抛物线C2交于点F.求证:
.将抛物线C1向下平移h个单位(h>0)得到抛物线C2.一条平行于x轴的直线与两条抛物线交于A、B、C、D四点(如图),且点A、C关于y轴对称,直线AB与x轴的距离是m2(m>0)。若抛物线C1的对称轴与直线AB交于点E,与抛物线C2交于点F.求证: =
=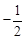 。
。
阅读下列材料:
我们知道,一次函数y=kx+b的图象是一条直线,而y=kx+b经过恒等变形可化为直线的另一种表达形式:Ax+Bx+C=0(A、B、C是常数,且A、B不同时为0).如图1,点P(m,n)到直线l:Ax+Bx+C=0的距离(d)计算公式是:d=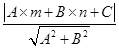 .
.

例:求点P(1,2)到直线y=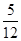 x-
x-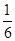 的距离d时,先将y=
的距离d时,先将y=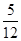 x-
x-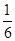 化为5x-12y-2=0,再由上述距离公式求得d=
化为5x-12y-2=0,再由上述距离公式求得d=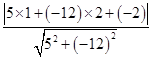 =
= .
.
解答下列问题:
如图2,已知直线y=-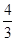 x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).
x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).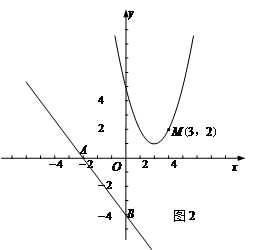

(1)求点M到直线AB的距离.
(2)抛物线上是否存在点P,使得△PAB的面积最小?若存在,求出点P的坐标及△PAB面积的最小值;若不存在,请说明理由.