（本小题满分12分）
如图，空间四边形ABCD被一平面所截，截面EFGH是平行四边形.
（1）求证：CD∥平面EFGH；
（2）如果AB=CD=a求证：四边形EFGH的周长为定值；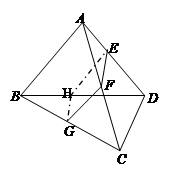
（本小题满分12分）设函数
的定义域为集合
，函数
的定义域为集合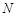
.
求：（1）集合
；
（2）集合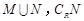
.
（本小题满分14分）已知二次函数
（
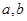为常数，
）的一个零点是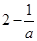
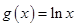.函数
，设函数
.
（1）求
的值，当
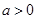时，求函数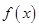
的单调增区间；
（2）当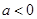
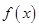时，求函数在区间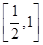
上的最小值；
（3）记函数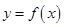
图象为曲线C，设点
是曲线C上不同的两点，点M为线段AB的中点，过点M作
轴的垂线交曲线C于点N.判断曲线C在点N处的切线是否平行于直线AB？并说明理由.
（本小题满分13分）某风景区在一个直径AB为100米的半圆形花园中设计一条观光线路（如图所示）.在点A与圆弧上的一点C之间设计为直线段小路，在路的两侧边缘种植绿化带；从点C到点B设计为沿弧BC的弧形小路，在路的一侧边缘种植绿化带.（注：小路及绿化带的宽度忽略不计）
（1）设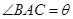
（弧度），将绿化带总长度表示为
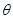的函数
；
（2）试确定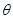的值，使得绿化带总长度最大.
（本小题满分12分）已知数列
满足
，等比数列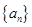
为递增数列，且
.
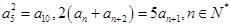（1）求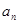
；
（2）令
，不等式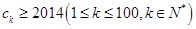
的解集为M，求所有
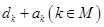的和.
（本小题满分12分）如图，在等腰梯形ABCD中，AB//CD，AD=DC=CB=1，∠ABC=60°，四边形ACFE为矩形，平面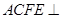
平面ABCD，CF=1.
（1）求证：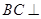
平面ACFE；
（2）点M在线段EF上运动，设平面MAB与平面FCB所成二面角的平面角为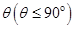
，试求
的取值范围.