(本小题满分14分)已知二次函数 (
(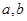 为常数,
为常数, )的一个零点是
)的一个零点是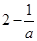 .函数
.函数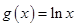 ,设函数
,设函数 .
.
(1)求 的值,当
的值,当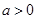 时,求函数
时,求函数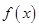 的单调增区间;
的单调增区间;
(2)当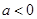 时,求函数
时,求函数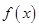 在区间
在区间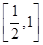 上的最小值;
上的最小值;
(3)记函数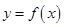 图象为曲线C,设点
图象为曲线C,设点 是曲线C上不同的两点,点M为线段AB的中点,过点M作
是曲线C上不同的两点,点M为线段AB的中点,过点M作 轴的垂线交曲线C于点N.判断曲线C在点N处的切线是否平行于直线AB?并说明理由.
轴的垂线交曲线C于点N.判断曲线C在点N处的切线是否平行于直线AB?并说明理由.
(本小题满分10分)选修4-1:几何证明选讲
如图, 是圆
是圆 的直径,
的直径, 是半径
是半径 的中点,
的中点, 是
是 延长线上一点,且
延长线上一点,且 ,直线
,直线 与圆
与圆 相交于点
相交于点 、
、 (不与
(不与 、
、 重合),
重合), 与圆
与圆 相切于点
相切于点 ,连结
,连结 ,
, ,
, .
.
(Ⅰ)求证: ;
;
(Ⅱ)若 ,求
,求 .
.
(本小题满分12分)已知函数 ,
, .
.
(Ⅰ)若 ,且
,且 存在单调递减区间,求
存在单调递减区间,求 的取值范围;
的取值范围;
(Ⅱ)设函数 的图象
的图象 与函数
与函数 的图象
的图象 交于点
交于点 、
、 ,过线段
,过线段 的中点
的中点 作
作 轴的垂线分别交
轴的垂线分别交 、
、 于点
于点 、
、 ,是否存在点
,是否存在点 ,使
,使 在点
在点 处的切线与
处的切线与 在点
在点 处的切线平行?如果存在,求出点
处的切线平行?如果存在,求出点 的横坐标,如果不存在,说明理由.
的横坐标,如果不存在,说明理由.
(本小题满分12分)已知椭圆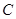 :
: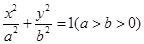 的焦点分别为
的焦点分别为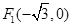 、
、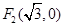 ,点
,点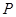 在椭圆
在椭圆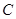 上,满足
上,满足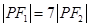 ,
,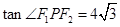 .
.
(Ⅰ)求椭圆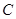 的方程;
的方程;
(Ⅱ)已知点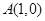 ,试探究是否存在直线
,试探究是否存在直线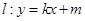 与椭圆
与椭圆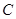 交于
交于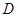 、
、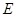 两点,且使得
两点,且使得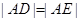 ?若存在,求出
?若存在,求出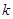 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(本小题满分12分)如图,在三棱柱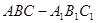 中,面
中,面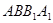 为矩形,
为矩形,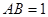 ,
,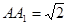 ,
,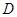 为
为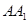 的中点,
的中点,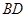 与
与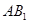 交于点
交于点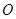 ,
,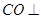 面
面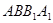 .
.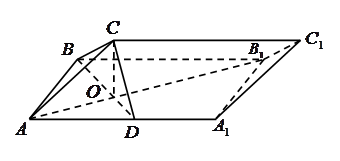
(Ⅰ)证明: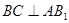 ;
;
(Ⅱ)若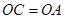 ,求二面角
,求二面角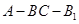 的余弦值.
的余弦值.
(本小题满分12分)某企业有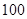 位员工.拟在新年联欢会中,增加一个摸球兑奖的环节,规定:每位员工从一个装有
位员工.拟在新年联欢会中,增加一个摸球兑奖的环节,规定:每位员工从一个装有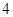 个标有面值的球的袋中一次性随机摸出
个标有面值的球的袋中一次性随机摸出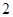 个球,球上所标的面值之和为该员工所获的中奖额.企业预算抽奖总额为
个球,球上所标的面值之和为该员工所获的中奖额.企业预算抽奖总额为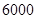 元,共提出两种方案.
元,共提出两种方案.
方案一:袋中所装的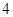 个球中有两个球所标的面值为
个球中有两个球所标的面值为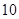 元,另外两个标的面值为
元,另外两个标的面值为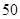 元;
元;
方案二:袋中所装的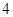 个球中有两个球所标的面值为
个球中有两个球所标的面值为 元,另外两个标的面值为
元,另外两个标的面值为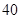 元.
元.
(Ⅰ)求两种方案中,某员工获奖金额的分布列;
(Ⅱ)在两种方案中,请帮助该企业选择一个适合的方案,并说明理由.