(本小题满分12分)某企业有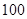 位员工.拟在新年联欢会中,增加一个摸球兑奖的环节,规定:每位员工从一个装有
位员工.拟在新年联欢会中,增加一个摸球兑奖的环节,规定:每位员工从一个装有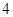 个标有面值的球的袋中一次性随机摸出
个标有面值的球的袋中一次性随机摸出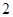 个球,球上所标的面值之和为该员工所获的中奖额.企业预算抽奖总额为
个球,球上所标的面值之和为该员工所获的中奖额.企业预算抽奖总额为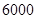 元,共提出两种方案.
元,共提出两种方案.
方案一:袋中所装的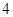 个球中有两个球所标的面值为
个球中有两个球所标的面值为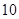 元,另外两个标的面值为
元,另外两个标的面值为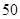 元;
元;
方案二:袋中所装的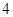 个球中有两个球所标的面值为
个球中有两个球所标的面值为 元,另外两个标的面值为
元,另外两个标的面值为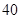 元.
元.
(Ⅰ)求两种方案中,某员工获奖金额的分布列;
(Ⅱ)在两种方案中,请帮助该企业选择一个适合的方案,并说明理由.
已知椭圆C: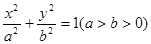 的一条准线L方程为:x=
的一条准线L方程为:x=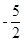 ,且左焦点F到L的距离为
,且左焦点F到L的距离为 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点F的直线交椭圆C于两点A、B,交L于点M,若 ,
,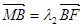 ,证明
,证明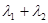 为定值.
为定值.
已知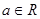 ,
,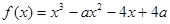 .
.
(Ⅰ)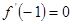 ,求函数
,求函数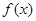 在区间
在区间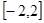 上的最大值与最小值;
上的最大值与最小值;
(Ⅱ)若函数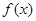 在区间
在区间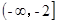 和
和 上都是增函数,求实数
上都是增函数,求实数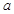 的取值范围.
的取值范围.
已知数列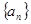 中,
中, ,
,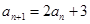 ,求数列
,求数列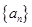 的通项公式.
的通项公式.
在某校举办的元旦有奖知识问答中,甲、乙、丙三人同时回答一道有关环保知识的问题,已知甲回答对这道题的概率是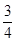 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是 .
.
(Ⅰ)求乙、丙两人各自回答对这道题的概率;
(Ⅱ)求甲、乙、丙三人同时回答这道题时至少有一人答错的概率.
叙述双曲线的定义,并建立适当的直角坐标系推导其标准方程.