1997年8月26日在日本举行的国际学术大会上，德国Max Plank学会的一个研究组宣布了他们的研究结果：银河系的中心可能存在一个大“黑洞”。“黑洞”是某些天体的最后演变结果。（引力常量G=6.67×10－11N·m2/kg2）
（1）根据长期观测发现，距离某“黑洞”6×1012m的另一个星体（设其质量为m）正以2×106m/s的速度绕“黑洞”旋转，求该“黑洞”的质量M（结果要求1位有效数字）；
（2）根据天体物理学知识，物体从某天体上的逃逸速度公式为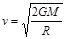
，其中G为引力常量，M为天体质量，R为天体半径，且已知逃逸速度大于真空中光速的天体叫“黑洞”，真空中光速c=3×108m/s，请估算（1）中“黑洞”可能的最大半径。（结果保留1位有效数字）
（本小题12分）在一个倾斜的长冰道上方，一群孩子排成队，每隔1s有一个小孩子往下滑，一游客对着冰道上的孩子拍下一张照片，如图所示照片上有甲．乙．丙．丁四个孩子。他根据照片与实物的比例推算出乙与甲和与丙两孩子间的距离分别为12．5 m和17．5 m，请你据此求解下列问题．（g取10 m/s2）
（1）若不考虑一切阻力，小孩下滑加速度是多少?
（2）拍照时，最下面的小孩丁的速度是多大?
（3）拍照时，在小孩甲上面的冰道上下滑的小孩子不会超过几个?
（本小题12分）如图所示，物重30 N，用OC绳悬挂在O点，OC绳能承受最大拉力为20
N，再用一绳系OC绳的A点，BA绳能承受的最大拉力为30 N，现用水平力拉BA，可以把OA绳拉到与竖直方向成多大角度?
在匀强电场中，将一电荷量为
的负电荷由
点移到
点，其电势能增加了
，已知、两点间距离为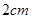
，两点连线与电场方向成
角，如图16所示，则：
（1）在电荷由移到的过程中，电场力做了多少功？
（2）、两点间的电势差为多少？
（3）该匀强电场的电场强度为多大？
如图所示，
为电阻箱，V为理想电压表。当电阻箱读数为
时，电压表读数为
；当电阻箱读数为
时，电压表读数为
。求：
（1）电源的电动势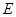
和内阻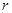
；
（2）当电阻箱读数为多少时，电源的输出功率最大？最大值为多少？
氢原子核外电子在与核的库仑力下做匀速圆周运动，若氢原子核外电子的轨道半径为
，电子质量为
，电量为
，求电子绕核运动的周期。（静电力常量为
）