解方程组: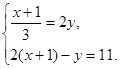
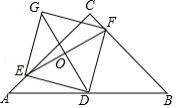
如图,在等腰直角三角形 中, , , 是 的中点, , 分别是 , 上的点(点 不与端点 , 重合),且 ,连接 并取 的中点 ,连接 并延长至点 ,使 ,连接 , , , .
(1)求证:四边形 是正方形;
(2)当点 在什么位置时,四边形 的面积最小?并求四边形 面积的最小值.
某新建成学校举行美化绿化校园活动,九年级计划购买 , 两种花木共100棵绿化操场,其中 花木每棵50元, 花木每棵100元.
(1)若购进 , 两种花木刚好用去8000元,则购买了 , 两种花木各多少棵?
(2)如果购买 花木的数量不少于 花木的数量,请设计一种购买方案使所需总费用最低,并求出该购买方案所需总费用.
如图, 是 的直径, 是上半圆的弦,过点 作 的切线 交 的延长线于点 ,过点 作切线 的垂线,垂足为 ,且与 交于点 ,设 , 的度数分别是 , .
(1)用含 的代数式表示 ,并直接写出 的取值范围;
(2)连接 与 交于点 ,当点 是 的中点时,求 , 的值.

在一个不透明的袋子中有一个黑球 和两个白球 , (除颜色外其他均相同).用树状图(或列表法)解答下列问题:
(1)小丽第一次从袋子中摸出一个球不放回,第二次又从袋子中摸出一个球.则小丽两次都摸到白球的概率是多少?
(2)小强第一次从袋子中摸出一个球,摸到黑球不放回,摸到白球放回;第二次又从袋子中摸出一个球,则小强两次都摸到白球的概率是多少?
已知关于 的一元二次方程: .
(1)求证:对于任意实数 ,方程都有实数根;
(2)当 为何值时,方程的两个根互为相反数?请说明理由.