有20筐白菜，以每筐25千克为标准，超过或不足的分别用正、负来表示，记录如下：
| 与标准质量的差（单位：千克） |
－3 |
－2 |
－1.5 |
0 |
1 |
2.5 |
| 筐数 |
1 |
4 |
2 |
3 |
2 |
8 |
（1）20筐白菜中，最重的一筐比最轻的一筐要重多少千克？
（2）与标准质量比较，20筐白菜总计超过或不足多少千克？
（3）若白菜每千克售价2.6元，则出售这20筐白菜可卖多少元？
如图1：直线y= kx+4k（k≠0）交x轴于点A，交y轴于点C，点M(2，m)为直线AC上一点，过点M的直线BD交x轴于点B，交y轴于点D．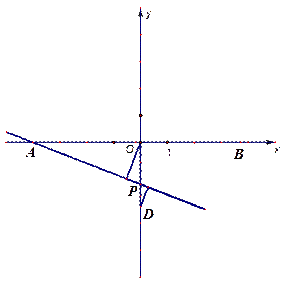
(1)求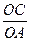
的值（用含有k的式子表示．）；
(2)若S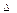
BOM =3S
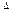DOM，且k为方程(k+7)(k+5)-(k+6)(k+5=
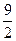的根，求直线BD的解析式．
(3)如图2，在(2)的条件下，P为线段OD之间的动点（点P不与点O和点D重合），OE
上AP于E，，DF上AP于F，下列两个结论：①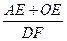
值不变；②
值不变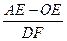，请你判断其中哪一个结论是正确的，并说明理由并求出其值，
如图1，AD∥BC，AB ⊥BC于B，∠DCB=75°，以CD为边的等边△DCE的另一顶点E在线段AB上．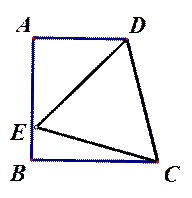
(1)填空：∠ADE=____°；
(2)求证： AB=BC;
(3)如图2所示，若F为线段CD上一点，∠FBC=30°，求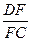
的值．
已知A、B两点在数轴上表示的数为a和b，M、N均为数轴上的点，且OA<OB．
(1)若A、B的位置如图l所示，试化简： 
-
+
+
(2)如图2，若+=8.9，MN=3，求图中以A、N、O、M、B这5个点为端点的所
有线段长度的和；
(3)如图3，M为AB中点，N为OA中点，且MN=2AB-15，a=-3，若点P为数轴上一点，且PA=
AB,试求点P所对应的数为多少？
已知：0为直线AB上的一点，射线OA表示正北方向，射线OC在北偏东m°的方向，射线OE在南偏东n°的方向，射线OF平分∠AOE，且2m+2n=180．
(1)如图1，∠ COE=______°， ∠COF和∠BOE之间的数量关系为________________.
(2)若将∠COE绕点O旋转至图2的位置，射线OF仍然平分∠AOE时，试问(1)中∠COF和∠BOE之间的数量关系是否发生变化？若不发生变化，请你加以证明，若发生变化，请你说明理由；
(3)若将∠COE绕点0旋转至图3位置，射线OF仍平分∠AOE时，则2 ∠COF+∠BOE= _°.
某人型超市元旦假期举行促销活动，规定一次购物不超过100元的不给优惠；超过100元而不超过300元时，按该次购物全额9折优惠；超过300元的其中300元仍按9折优惠，超过部分按8折优惠；小美第第一次购物用了94.5元，第二次购物用了282.8元．
(1)小美第一次购物的原价为多少？
(2)小美第二次购物的原价为多少元？