(本小题满分12分)某家具厂有方木料90 ,五合板600
,五合板600 ,准备加工成书桌和书橱出售。已知生产每张书桌需要方木料0.1
,准备加工成书桌和书橱出售。已知生产每张书桌需要方木料0.1 、五合板2
、五合板2 ;生产每个书橱需要方木料0.2
;生产每个书橱需要方木料0.2 、五合板1
、五合板1 . 出售一张书桌可获利润80元,出售一个书橱可获利润120元,怎样安排生产可使所得利润最大?
. 出售一张书桌可获利润80元,出售一个书橱可获利润120元,怎样安排生产可使所得利润最大?
(本小题满分14分)某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
| 组号 |
第一组 |
第二组 |
第三组 |
第四组 |
第五组 |
| 分组 |
[50,60) |
[60,70) |
[70,80) |
[80,90) |
[90,100] |
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;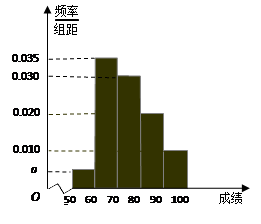
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率?
(本小题满分13分)设关于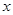 的一元二次方程
的一元二次方程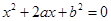 .
.
(1)若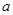 是从
是从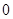 、
、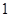 、
、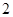 、
、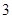 四个数中任取的一个数,
四个数中任取的一个数,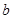 是从
是从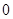 、
、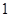 、
、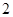 三个数中任取的一个数,求上述方程有实根的概率;
三个数中任取的一个数,求上述方程有实根的概率;
(2)若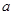 是从区间
是从区间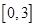 任取的一个数,
任取的一个数,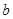 是从区间
是从区间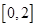 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
(本小题满分13分)如图,∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,试求: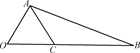
(1)△AOC为钝角三角形的概率;
(2)△AOC为锐角三角形的概率.
(本小题满分13分)据预测,某旅游景区游客人数在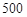 至
至 人之间,游客人数
人之间,游客人数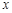 (人)与游客的消费总额
(人)与游客的消费总额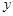 (元)之间近似地满足关系:
(元)之间近似地满足关系: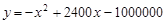
(1)若该景区游客消费总额不低于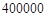 元时,求景区游客人数的范围。
元时,求景区游客人数的范围。
(2)当景区游客的人数为多少人时,游客的人均消费最高?并求游客的人均最高消费额。
(参考公式:当a>0,b>0时,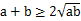 ,当且仅当a=b时等号成立)
,当且仅当a=b时等号成立)
(本小题满分13分) 已知集合 ,
,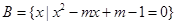 .若
.若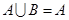 ,求实数
,求实数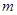 的取值范围.
的取值范围.