(本题满分14分 )如图,在三棱柱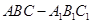 中,所有的棱长都为2,
中,所有的棱长都为2, .
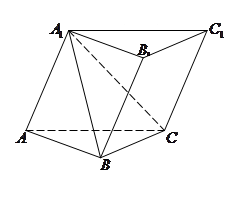
.
(1)求证: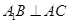 ;
;
(2)当三棱柱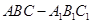 的体积最大时,
的体积最大时,
求平面 与平面
与平面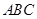 所成的锐角的余弦值.
所成的锐角的余弦值.
选修4-1:几何证明选讲
如图,过圆O外一点M作它的一条切线,切点为A,过A作直线AP⊥OM于P.
(1)证明: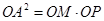 ;
;
(2)N为线段AP上一点,直线NB⊥ON且交圆O于B点,过B点的切线交直线ON于K.证明:∠OKM=90°.
已知函数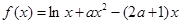 ,其中a为常数,且
,其中a为常数,且 .
.
(1)当a=1时,求f(x)的单调区间;
(2)若f(x)在x=1处取得极值,且在(0,e]上的最大值为1,求a的值.
已知椭圆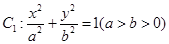 的右焦点与抛物线
的右焦点与抛物线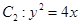 的焦点F重合,椭圆
的焦点F重合,椭圆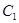 与抛物线
与抛物线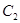 在第一象限的交点为P,
在第一象限的交点为P, .
.
(1)求椭圆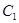 的方程;
的方程;
(2)过点A(-1,0)的直线与椭圆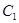 相交于M,N两点,求使
相交于M,N两点,求使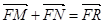 成立的动点R的轨迹方程.
成立的动点R的轨迹方程.
一次考试中,5名同学的语文、英语成绩如下表所示: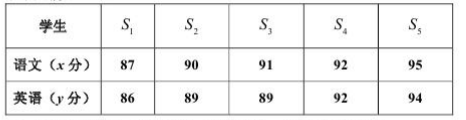
(1)根据表中数据,求英语分y对语文分x的线性回归方程;
(2)要从4名语文成绩在90分(含90分)以上的同学中选出2名参加一项活动,以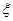 表示选中的同学的英语成绩高于90分的人数,求随机变量
表示选中的同学的英语成绩高于90分的人数,求随机变量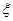 的分布列及数学期望
的分布列及数学期望 .
.
(线性回归方程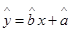 ,
,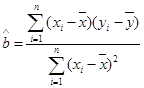 ,
,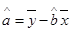 ,其中
,其中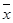 ,
,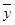 为样本平均值,
为样本平均值,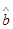 ,
,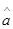 的值的结果保留二位小数.)
的值的结果保留二位小数.)
如图,在长方体 中,
中, ,AB=2,点E是线段AB的中点.
,AB=2,点E是线段AB的中点.
(1)求证: ;
;
(2)求二面角 的大小的余弦值.
的大小的余弦值.