阅读下面的文字,解答问题.
大家知道
是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部地写出来,于是小明用-1来表示的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理的,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.
请解答:已知:10+
=x+y,其中x是整数,且0<y<1,求x-y的相反数.
如图，已知AC，EC分别为正方形ABCD和正方形EFCG的对角线，点E在△ABC内，连接BF，∠CAE+∠CBE=90°．
（1）求证：△CAE∽△CBF；
（2）若BE=1，AE=2，求CE的长．
小明和小刚做游戏，用一个不透明袋子，里面装有形状、大小完全相同的2个红球和2个白球，并充分搅匀，让小刚从中摸出一个球不放回，再去摸第二个球，如果两次摸出的球颜色相同小刚赢，反之小明赢．你认为这种游戏是否公平？请你借助树状图或列表的方法，运用概率的知识予以说明．
如图，在宽为20米、长为30米的矩形地面上修建两条同样宽的道路，余下部分作为耕地．若耕地面积需要551米2，则修建的路宽应为多少米？
如图，在▱ABCD中，∠ABD的平分线BE交AD于点E，∠CDB的平分线DF交BC于点F，连接BD．
（1）求证：△ABE≌△CDF；
（2）若AB=DB，求证：四边形DFBE是矩形．
如图，△ABC中，CD是边AB上的高，且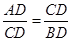
．
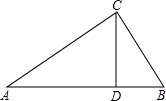
（1）求证：△ACD∽△CBD；
（2）求∠ACB的大小．