在边长为16cm的正方形纸片的四个角各剪去一个同样大小的正方形，折成一个无盖的长方体．
（1）如果剪去的小正方形的边长为xcm，请用含x的代数式来表示这个无盖长方体的体积；
（2）当剪去的小正方形的边长x的值分别为3cm和3．5cm时，比较折成的无盖长方体的体积的大小．
先化简，再求值：
，其中
．
画一条数轴，并在数轴上表示：3．5和它的相反数，－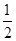
和它的倒数，绝对值等于3的数，并把这些数由小到大用“<”号连接起来．
若|a|=4，|b|=2，且a＜b，求a－b的值．
已知：如图，平面直角坐标系中，矩形OABC的顶点A（6，0）、B（6，4），D是BC的中点．动点P从O点出发，以每秒1个单位的速度，沿着OA、AB、BD运动．设P点运动的时间为t秒（0<t<13）．
（1）写出△POD的面积S与t之间的函数关系式，并求出△POD的面积等于9时点P的坐标；
（2）当点P在OA上运动时，连结CP．问：是否存在某一时刻t，当CP绕点P旋转时，点C能恰好落到AB的中点M处？若存在，请求出t的值并判断此时△CPM的形状；若不存在，请说明理由；
（3）当点P在AB上运动时，试探索当PO+PD的长最短时的直线PD的表达式。
满足条件:a2＋b2＋c2＋338＝10a＋24b＋26c，试判断△ABC的形状．