某中学为了了解七年级男生入学时的跳绳情况,随机选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图(如图所示).根据图表解答下列问题:
⑴ a=,b=;
⑵ 这个样本数据的中位数落在第组;
⑶ 若七年级男生个人一分钟跳绳次数x≥130时成绩为优秀,则从这50名男生中任意选一人,跳绳成绩为优秀的概率为多少?
⑷ 若该校七年级入学时男生共有150人,请估计此时该校七年级男生个人一分钟跳绳成绩为优秀的人数.
如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连接DE.
(1)求证:△ABE≌△DFA;
(2)如果AD=10,AB=6,求sin∠EDF的值.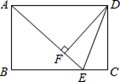
解方程: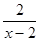 -
-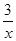 =1
=1
解不等式组:
化简: