在四边形ABCD中,对角线AC、BD交于点O且|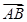 |=|
|=|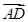 |=1,
|=1, +
+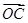 =
=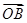 +
+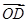 =0,cos∠DAB=
=0,cos∠DAB=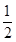 .求|
.求|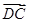 +
+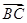 |与|
|与|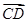 +
+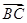 |.
|.
求函数f(x)=lgsin x+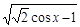 的定义域.
的定义域.
已知关于 的方程
的方程 =1,其中
=1,其中 为实数.
为实数.
(1)若 =1-
=1-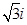 是该方程的根,求
是该方程的根,求 的值.
的值.
(2)当 >
>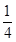 且
且 >0时,证明该方程没有实数根.
>0时,证明该方程没有实数根.
从三角形内部任意一点向各边引垂线,其长度分别为 ,且相应各边上的高分别为
,且相应各边上的高分别为 ,求证:
,求证: =1.类比以上性质,给出空间四面体的一个猜想,并给出证明.
=1.类比以上性质,给出空间四面体的一个猜想,并给出证明.
建立数学模型一般都要经历下列过程:从实际情境中提出问题,建立数学模型,通过计算或推导得到结果,结合实际情况进行检验.如果合乎实际,就得到可以应用的结果,否则重新审视问题的提出、建模、计算和推导得到结果的过程,直到得到合乎实际的结果为止.请设计一个流程图表示这一过程.
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人. 女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2的列联表.
(2)能否在犯错误的概率不超过0.025的前提下,认为性别与休闲方式有关系?