已知在公比为实数的等比数列 中,
中,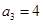 ,且
,且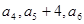 成等差数列.
成等差数列.
(1) 求数列 的通项公式;
的通项公式;
(2) 设数列 的前n项和为Sn,求S10.
的前n项和为Sn,求S10.
(1)用数学归纳法证明等式1+2+3+…+(n+3)=  .
.
(2)用数学归纳法证明不等式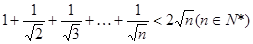 .
.
中日“钓鱼岛争端”问题越来越引起社会关注,我校对高一600名学生进行了一次“钓鱼岛”知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
填写答题卡频率分布表中的空格,补全频率分布直方图,并标出每个小矩形
对应的纵轴数据;
(2)请你估算该年级的平均数及中位数.
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作四次试验,得到的数据如下:
| 零件的个数x(个) |
2 |
3 |
4 |
5 |
| 加工的时间y(小时) |
2.5 |
3 |
4 |
4.5 |
(1)已知零件个数与加工时间线性相关,求出y关于x的线性回归方程;
(2)试预测加工10个零件需要多少时间?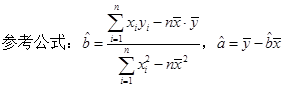
用秦九韶算法求多项式f(x)=2x5-5x4-4x3+3x2-6x+7当x=5时的值.
甲有大小相同的两张卡片,标有数字2、3;乙有大小相同的卡片四张,分别标有1、2、3、4.
(1)求乙随机抽取的两张卡片的数字之和为奇数的概率;
(2)甲、乙分别取出一张卡,比较数字,数字大者获胜,求乙获胜的概率.