甲、乙、丙三人独立破译同一份密码,已知甲、乙、丙各自破译出密码的概率分别为 、
、 、
、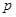 ,且他们是否破译出密码互不影响,若三人中只有甲破译出密码的概率为
,且他们是否破译出密码互不影响,若三人中只有甲破译出密码的概率为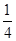 .
.
(1)求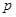 的值.
的值.
(2)设甲、乙、丙三人中破译出密码的人数为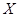 ,求
,求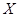 的分布列和数学期望
的分布列和数学期望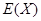 .
.
(本小题满分12分)
如图,FD垂直于矩形ABCD所在平面,CE//DF,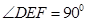 .
.
(Ⅰ)求证:BE//平面ADF;
(Ⅱ)若矩形ABCD的一个边AB =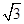 ,EF =
,EF =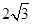 ,则另一边BC的长为何值时,二面角B-EF-D的大小为450?
,则另一边BC的长为何值时,二面角B-EF-D的大小为450?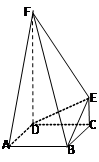
(本小题满分12分)
三角形的三个内角A、B、C所对边的长分别为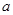 、
、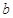 、
、 ,设向量
,设向量 ,若
,若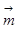 //
//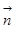 .
.
(I)求角B的大小;
(II)求 的取值范围.
的取值范围.
(本小题满分15分)如图,在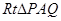 中,点
中,点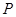 的坐标为
的坐标为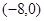 ,点
,点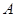 在
在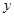 轴上,点
轴上,点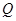 在
在 轴的正半轴上,
轴的正半轴上, ,在
,在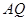 的延长线上取一点
的延长线上取一点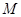 ,使
,使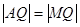 .
.
(Ⅰ)当点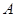 在
在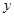 轴上移动时,求动点
轴上移动时,求动点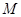 的轨迹
的轨迹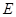 ;
;
(Ⅱ)自点 引直线与轨迹
引直线与轨迹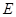 交于不同的两点
交于不同的两点 、
、 ,点
,点 关于
关于 轴的对称点
轴的对称点
记为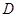 ,设
,设 ,点
,点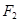 的坐标为
的坐标为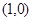 .
.
(1)求证: ;
;
(2)若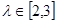 ,求
,求 的取值范围.
的取值范围.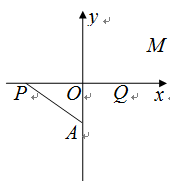
(本小题满分15分)如图,在三棱柱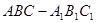 中,已知
中,已知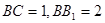 ,
,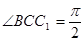 ,
, .
.
(Ⅰ)求直线 与底面
与底面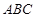 所成角正切值;
所成角正切值;
(Ⅱ)在棱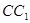 (不包含端点)上确定一点
(不包含端点)上确定一点 的位置,
的位置,
使得 (要求说明理由);
(要求说明理由);
(Ⅲ)在(Ⅱ)的条件下,若 ,求二面角
,求二面角 的大小.
的大小.
(本小题满分14分)已知椭圆 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在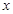 轴上,椭圆上的点到
轴上,椭圆上的点到
两个焦点的距离之和为 ,离心率
,离心率 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设椭圆 的左、右焦点分别为
的左、右焦点分别为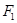 、
、 ,过点
,过点 的直线
的直线 与该椭圆交于点
与该椭圆交于点 、
、 ,
,
以 、
、 为邻边作平行四边形
为邻边作平行四边形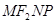 ,求该平行四边形对角线
,求该平行四边形对角线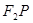 的长度
的长度
的最大值.