已知圆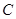 的极坐标方程是
的极坐标方程是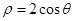 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为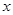 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线 的参数方程为
的参数方程为 (
(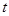 为参数).若直线
为参数).若直线 与圆
与圆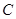 相交于
相交于 ,
,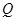 两点,且
两点,且 .
.
(Ⅰ)求圆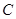 的直角坐标方程,并求出圆心坐标和半径;
的直角坐标方程,并求出圆心坐标和半径;
(Ⅱ)求实数 的值.
的值.
(本小题满分8分)已知

(1)当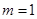 时,求
时,求 ;
;
(2) 若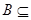
 ,求实数
,求实数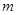 的取值范围.
的取值范围.
(本小题10分)已知函数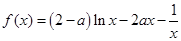 .
.
(1)试讨论 的单调性;
的单调性;
(2)如果当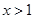 时,
时,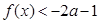 ,求实数
,求实数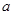 的取值范围;
的取值范围;
(3)记函数 ,若
,若 在区间
在区间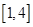 上不单调, 求实数
上不单调, 求实数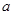 的取值范围.
的取值范围.
(本小题8分)自主招生是高校在高考前争抢优等生的一项重要举措,不少同学也把自主招生当作高考前的一次锻炼.据参加自主招生的某同学说,某高校2012自主招生选拔考试分为初试和面试两个阶段,参加面试的考生按照抽签方式决定出场顺序.通过初试,选拔出甲、乙等五名考生参加面试.
(1)求面试中甲、乙两名考生恰好排在前两位的概率;
(2)若面试中甲和乙之间间隔的考生数记为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(本小题8分)已知数列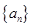 中,
中, ,且
,且 .
.
(1)求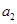 ,
, ,
, 的值;
的值;
(2)写出数列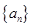 的通项公式,并用数学归纳法证明.
的通项公式,并用数学归纳法证明.
(本小题8分)在二项式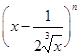 的展开式中,前三项系数的绝对值成等差数列.
的展开式中,前三项系数的绝对值成等差数列.
(1)求展开式的常数项; (2)求展开式中二项式系数最大的项的系数;
(3)求展开式中各项的系数和.