(本小题10分)已知函数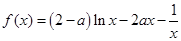 .
.
(1)试讨论 的单调性;
的单调性;
(2)如果当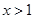 时,
时,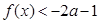 ,求实数
,求实数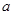 的取值范围;
的取值范围;
(3)记函数 ,若
,若 在区间
在区间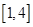 上不单调, 求实数
上不单调, 求实数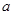 的取值范围.
的取值范围.
设数列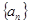 的各项都是正数,且对任意
的各项都是正数,且对任意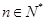 ,都有
,都有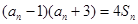 ,其中
,其中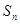 为数列
为数列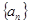 的前
的前 项和。
项和。
(1)求证数列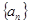 是等差数列;
是等差数列;
(2)若数列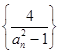 的前
的前 项和为Tn,求Tn。
项和为Tn,求Tn。
在 中,边
中,边 、
、 、
、 分别是角
分别是角 、
、 、
、 的对边,且满足
的对边,且满足
(1)求 ;
;
(2)若 ,
, ,求边
,求边 ,
, 的值.
的值.
已知偶函数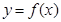 满足:当
满足:当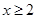 时,
时,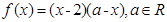 ,当
,当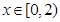 时,
时,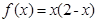 .
.
(Ⅰ)求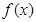 表达式;
表达式;
(Ⅱ)若直线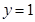 与函数
与函数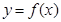 的图像恰有两个公共点,求实数
的图像恰有两个公共点,求实数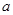 的取值范围;
的取值范围;
(Ⅲ)试讨论当实数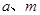 满足什么条件时,直线
满足什么条件时,直线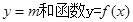 的图像恰有
的图像恰有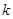 个公共点
个公共点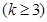 ,且这
,且这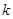 个公共点均匀分布在直线
个公共点均匀分布在直线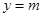 上.(不要求过程)
上.(不要求过程)
如图,斜率为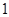 的直线过抛物线
的直线过抛物线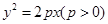 的焦点,与抛物线交于两点A、B, M为抛物线弧AB上的动点.
的焦点,与抛物线交于两点A、B, M为抛物线弧AB上的动点.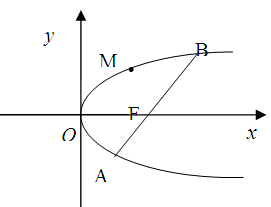
(Ⅰ)若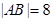 ,求抛物线的方程;
,求抛物线的方程;
(Ⅱ)求△ABM面积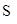 的最大值.
的最大值.
已知函数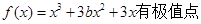
(Ⅰ)求函数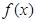 的单调区间及
的单调区间及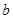 的取值范围;
的取值范围;
(Ⅱ)若函数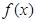 有两个极值点
有两个极值点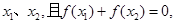 求
求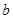 的值.
的值.