(本小题满分13分)如图(甲),在直角梯形ABED中,AB//DE,AB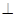 BE,AB
BE,AB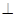 CD,且BC=CD,AB=2,F、H、G分别为AC ,AD ,DE的中点,现将△ACD沿CD折起,使平面ACD
CD,且BC=CD,AB=2,F、H、G分别为AC ,AD ,DE的中点,现将△ACD沿CD折起,使平面ACD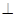 平面CBED,如图(乙).
平面CBED,如图(乙).
(1)求证:平面FHG//平面ABE;
(2)记
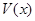 表示三棱锥B-ACE 的体积,求
表示三棱锥B-ACE 的体积,求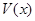 的最大值;
的最大值;
(3)当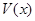 取得最大值时,求二面角D-AB-C的余弦值.
取得最大值时,求二面角D-AB-C的余弦值.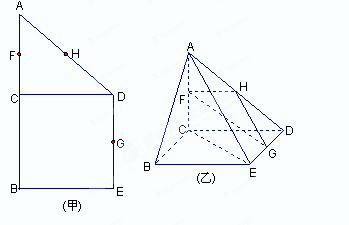
已知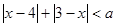
(1)若不等式的解集为空集,求 的范围;
的范围;
(2)若不等式有解,求 的范围。
的范围。
已知直线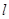 是过点
是过点 ,方向向量为
,方向向量为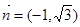 的直线。圆方程
的直线。圆方程
(1)求直线l的参数方程;
(2)设直线l与圆相交于 、
、 两点,求
两点,求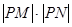 的值。
的值。
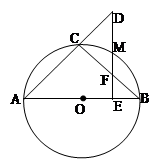
如图, 是圆
是圆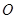 的直径,
的直径, 为圆上一点,
为圆上一点, ,垂足为
,垂足为 ,点
,点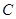 为圆
为圆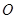 上任一点,
上任一点,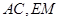 交于点
交于点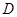 ,
,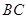 交
交 于点
于点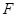 .
.
求证:(1)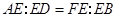 ;(2)
;(2) .
.
已知函数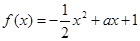 ,
,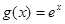 ,
,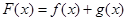 .
.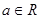
(1)若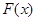 在
在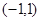 存在极值,求
存在极值,求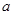 的取值范围;
的取值范围;
(2)若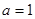 ,问是否存在与曲线
,问是否存在与曲线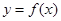 和
和 都相切的直线?若存在,判断有几条?并求出公切线方程,若不存在,说明理由。
都相切的直线?若存在,判断有几条?并求出公切线方程,若不存在,说明理由。
椭圆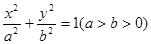 与
与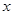 轴负半轴交于点
轴负半轴交于点 ,
,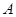 为椭圆第一象限上的点,直线
为椭圆第一象限上的点,直线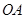 交椭圆于另一点
交椭圆于另一点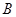 ,椭圆左焦点为
,椭圆左焦点为 ,连接
,连接 交
交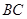 于点D。
于点D。
(1)如果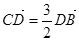 ,求椭圆的离心率;
,求椭圆的离心率;
(2)在(1)的条件下,若直线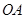 的倾斜角为
的倾斜角为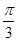 且△ABC的面积为
且△ABC的面积为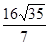 ,求椭圆的标准方程。
,求椭圆的标准方程。