标准方程下的椭圆的短轴长为 ,焦点
,焦点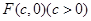 ,右准线
,右准线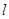 与
与 轴相交于点
轴相交于点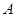 ,且
,且 ,过点
,过点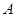 的直线和椭圆相交于点
的直线和椭圆相交于点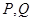 .
.
(1)求椭圆的方程和离心率;
(2)若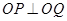 ,求直线
,求直线 的方程.
的方程.
(本小题满分13分)已知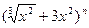 的展开式中,名项系数的和与其各项二项式系数的和之比为32
的展开式中,名项系数的和与其各项二项式系数的和之比为32
(Ⅰ)求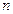
(Ⅱ)求展开式中二项式系数最大的项
(本小题满分13分)如图,正三棱柱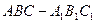 的所有棱长都为2,
的所有棱长都为2,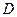 为
为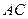 的中点。
的中点。
(Ⅰ)求证: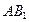 ∥平面
∥平面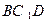 ;
;
(Ⅱ)求异面直线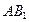 与
与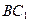 所成的角。
所成的角。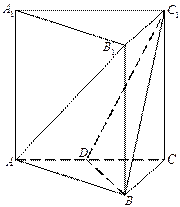
如图,在半径为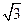 、圆心角为
、圆心角为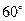 的扇形的弧上任取
的扇形的弧上任取 一点
一点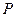 ,作扇
,作扇 形的内接矩形
形的内接矩形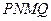 ,使点
,使点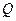 在
在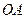 上,点
上,点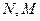 在
在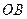 上,设矩形
上,设矩形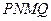 的面积为
的面积为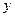 ,
,
(1)按下列要求写出函数的关系式:
①设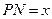 ,将
,将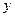 表示成
表示成 的函数关系式;
的函数关系式;
②设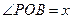 ,将
,将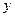 表
表 示成
示成 的函数关系式,
的函数关系式,
(2)请你选用(1)中的一个函数关系式,求出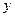 的最大值。
的最大值。
已知函数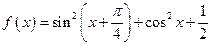 ,
,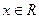
(1)求函数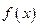 最值与最小
最值与最小 正周期;
正周期;
(2)求使不等式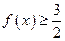
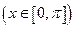 成立的
成立的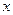 的取值范围。
的取值范围。
已知 的图像与
的图像与 轴的交点为
轴的交点为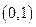 ,它在
,它在 轴右侧的第一个最大值和最小值点分别为
轴右侧的第一个最大值和最小值点分别为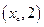 和
和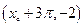
(1)求 的解析式;
的解析式;
(2)求 的单调递增区间
的单调递增区间
(3)将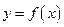 的图像上所有点的横坐标变为原来的
的图像上所有点的横坐标变为原来的 ,再将所得图像向右平移
,再将所得图像向右平移 个单位得函数
个单位得函数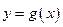 的图像,求
的图像,求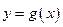 的解析式。
的解析式。