已知 ,
,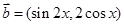 ,且
,且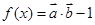
(1)求函数
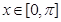 的单调增区间;
的单调增区间;
(2)证明无论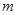 为何值,直线
为何值,直线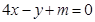 与函数
与函数 的图象不相切.
的图象不相切.
某食品企业一个月内被消费者投诉的次数用 表示,椐统计,随机变量
表示,椐统计,随机变量 的概率分布如下:
的概率分布如下:
 |
0 |
1 |
2 |
3 |
| p |
0.1 |
0.3 |
2a |
a |
(1)求a的值和 的数学期望;
的数学期望;
(2)假设一月份与二月份被消费者投诉的次数互不影响,求该企业在这两个月内共被消费者投诉2次的概率.
已知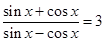 .
.
(1)求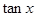 的值;
的值;
(2)若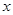 是第三象限的角,化简三角式
是第三象限的角,化简三角式 ,并求值.
,并求值.
(本小题满分14分)已知函数 .
.
(l)求 的单调区间和极值;
的单调区间和极值;
(2)若对任意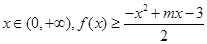 恒成立,求实数m的最大值.
恒成立,求实数m的最大值.
在△ABC中,a、b、c分别为内角A、B、C的对边,且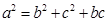 .
.
(1)求A的大小;
(2)若 ,试求△ABC的面积.
,试求△ABC的面积.