(本小题满分14分) 如图,已知抛物线与坐标轴分别交于A 、B
、B 、C
、C 三点,过坐标原点O的直线
三点,过坐标原点O的直线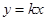 与抛物线交于M、N两点.分别过点C、D
与抛物线交于M、N两点.分别过点C、D 作平行于
作平行于 轴的直线
轴的直线 、
、 .(1)求抛物线对应的二次函数的解析式;
.(1)求抛物线对应的二次函数的解析式;
(2)求证以ON为直径的圆与直线 相切;
相切;
(3)求线段MN的长(用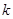 表示),并证明M、N两
表示),并证明M、N两
点到直线 的距离之和等于线段MN的长.
的距离之和等于线段MN的长.
已知二次函数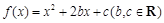 满足
满足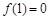 ,且关于
,且关于 的
的
方程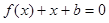 的两个实数根分别在区间
的两个实数根分别在区间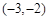 、
、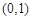 内.
内.
(1)求实数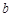 的取值范围;
的取值范围;
(2)若函数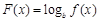 在区间
在区间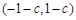 上具有单调性,求实数
上具有单调性,求实数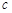 的取值范围.
的取值范围.
(本小题满分15分)在四棱锥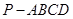 中,
中, 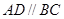 ,
,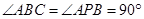 ,点
,点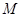 是线段
是线段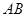 上的一点,且
上的一点,且 ,
,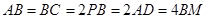 .
.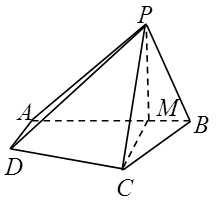
(1)证明:面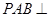 面
面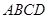 ;
;
(2)求直线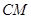 与平面
与平面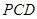 所成角的正弦值.
所成角的正弦值.
(本小题满分14分)已知等差数列 的前
的前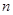 项和为
项和为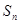 ,且
,且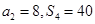 .数列
.数列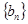 的前
的前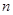 项和为
项和为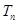 ,且
,且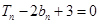 ,
,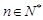 .
.
(Ⅰ)求数列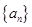 ,
,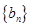 的通项公式;
的通项公式;
(Ⅱ)设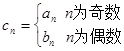 , 求数列
, 求数列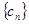 的前
的前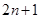 项和
项和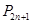 .
.
在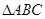 中,角
中,角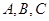 的对边分别为
的对边分别为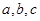 ,且
,且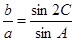 .
.
(1)若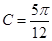 ,求角
,求角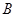 的大小;
的大小;
(2)若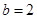 ,
,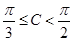 ,求
,求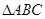 面积的最小值.
面积的最小值.
(本小题满分14分)已知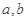 是实数,函数
是实数,函数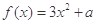 ,
,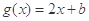 ,若
,若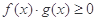 在区间
在区间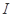 上恒成立,则称
上恒成立,则称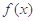 和
和 在区间
在区间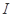 上为“
上为“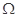 函数”.
函数”.
(1)设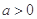 ,若
,若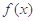 和
和 在区间
在区间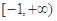 上为“
上为“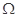 函数”,求实数
函数”,求实数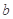 的取值范围;
的取值范围;
(2)设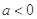 且
且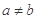 ,若
,若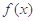 和
和 在以
在以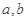 为端点的开区间上为“
为端点的开区间上为“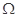 函数”,求
函数”,求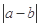 的最大值.
的最大值.