动点P从边长为1的正方形ABCD的顶点A出发顺次经过B、C、D再回到A. 设 表示P点的行程,
表示P点的行程,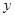 表示PA的长,求
表示PA的长,求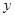 关于
关于 的函数解析式
的函数解析式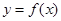 。
。
已知函数f(x)= sin
sin .
.
(1)求它的振幅、周期、初相;
(2)在所给坐标系中用五点法作出它在区间 上的图象.
上的图象.
(3)说明y=sin x的图像可由y= sin
sin 的图像经过怎样的变换而得到.
的图像经过怎样的变换而得到.
如图,函数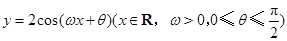 的图象与
的图象与 轴相交于点
轴相交于点 ,且该函数的最小正周期为
,且该函数的最小正周期为 .
.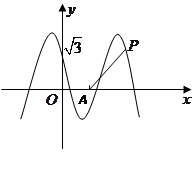
(1)、求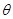 和
和 的值;
的值;
(2)、已知点 ,点
,点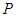 是该函数图象上一点,
是该函数图象上一点,
点 是
是 的中点,当
的中点,当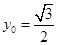 ,
, 时,求
时,求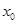 的值.
的值.
已知数列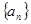 的前
的前 项和为
项和为 ,且满足
,且满足 (
(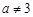 ),
), ,设
,设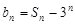 ,
,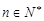 .
.
(1)求证:数列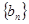 是等比数列;
是等比数列;
(2)若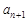 ≥
≥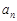 ,
,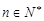 ,求实数
,求实数 的最小值;
的最小值;
(3)当 时,给出一个新数列
时,给出一个新数列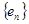 ,其中
,其中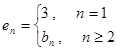 ,设这个新数列的前
,设这个新数列的前 项和为
项和为 ,若
,若 可以写成
可以写成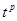 (
(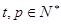 且
且 )的形式,则称
)的形式,则称 为“指数型和”.问
为“指数型和”.问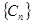 中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由.
中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由.
已知点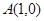 ,
, 、
、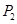 、
、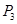 是平面直角坐标系上的三点,且
是平面直角坐标系上的三点,且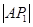 、
、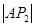 、
、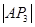 成等差数列,公差为
成等差数列,公差为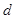 ,
,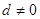 .
.
(1)若 坐标为
坐标为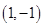 ,
,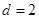 ,点
,点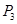 在直线
在直线 上时,求点
上时,求点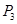 的坐标;
的坐标;
(2)已知圆 的方程是
的方程是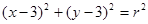
 ,过点
,过点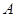 的直线交圆于
的直线交圆于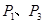 两点,
两点,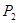 是圆
是圆 上另外一点,求实数
上另外一点,求实数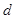 的取值范围;
的取值范围;
(3)若 、
、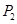 、
、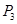 都在抛物线
都在抛物线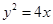 上,点
上,点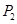 的横坐标为
的横坐标为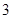 ,求证:线段
,求证:线段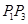 的垂直平分线与
的垂直平分线与 轴的交点为一定点,并求该定点的坐标.
轴的交点为一定点,并求该定点的坐标.
已知函数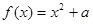 .
.
(1)若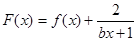 是偶函数,在定义域上
是偶函数,在定义域上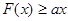 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(2)当 时,令
时,令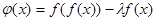 ,问是否存在实数
,问是否存在实数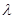 ,使
,使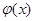 在
在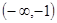 上是减函数,在
上是减函数,在 上是增函数?如果存在,求出
上是增函数?如果存在,求出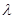 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.