(本小题满分14分)有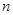 个首项都是1的等差数列,设第
个首项都是1的等差数列,设第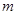 个数列的第
个数列的第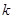 项为
项为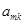
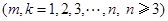 ,公差为
,公差为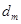 ,并且
,并且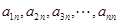 成等差数列.
成等差数列.
(Ⅰ)证明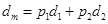 (
(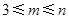 ,
,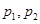 是
是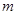 的多项式),并求
的多项式),并求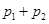 的值;
的值;
(Ⅱ)当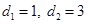 时,将数列
时,将数列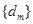 分组如下:
分组如下: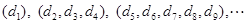 (每组数的个数构成等差数列).设前
(每组数的个数构成等差数列).设前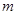 组中所有数之和为
组中所有数之和为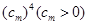 ,求数列
,求数列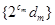 的前
的前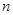 项和
项和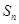 .
.
(Ⅲ)设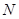 是不超过20的正整数,当
是不超过20的正整数,当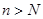 时,对于(Ⅱ)中的
时,对于(Ⅱ)中的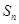 ,求使得不等式
,求使得不等式 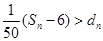 成立的所有
成立的所有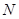 的值.
的值.
(本小题满分14分)已知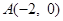 ,
, 为椭圆
为椭圆 的左、右顶点,
的左、右顶点,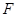 为其右焦点,
为其右焦点,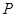 是椭圆
是椭圆 上异于
上异于 ,
,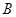 的动点,且
的动点,且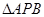 面积的最大值为
面积的最大值为 .
.
(Ⅰ)求椭圆 的方程及离心率;
的方程及离心率;
(Ⅱ)直线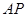 与椭圆在点
与椭圆在点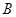 处的切线交于点
处的切线交于点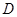 ,当直线
,当直线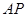 绕点
绕点 转动时,试判断以
转动时,试判断以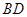 为直径的圆与直线
为直径的圆与直线 的位置关系,并加以证明.
的位置关系,并加以证明.
(本小题满分13分)已知函数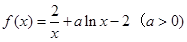 .
.
(Ⅰ)若曲线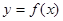 在点
在点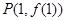 处的切线与直线
处的切线与直线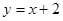 垂直,求函数
垂直,求函数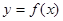 的单调区间;
的单调区间;
(Ⅱ)若对于 都有
都有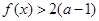 成立,试求
成立,试求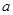 的取值范围;
的取值范围;
(Ⅲ)记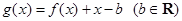 .当
.当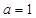 时,函数
时,函数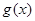 在区间
在区间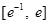 上有两个零点,求实数
上有两个零点,求实数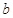 的取值范围.
的取值范围.
(本小题满分13分)在某校教师趣味投篮比赛中,比赛规则是: 每场投6个球,至少投进4个球且最后2个球都投进者获奖;否则不获奖.已知教师甲投进每个球的概率都是 .
.
(Ⅰ)记教师甲在每场的6次投球中投进球的个数为X,求X的分布列及数学期望;
(Ⅱ)求教师甲在一场比赛中获奖的概率;
(Ⅲ)已知教师乙在某场比赛中,6个球中恰好投进了4个球,求教师乙在这场比赛中获奖的概率;教师乙在这场比赛中获奖的概率与教师甲在一场比赛中获奖的概率相等吗?
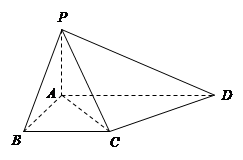
(本小题满分13分)如图,在四棱锥 中,底面
中,底面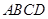 为直角梯形,且
为直角梯形,且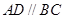 ,
,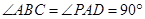 ,侧面
,侧面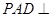 底面
底面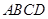 .若
.若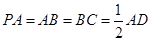 .
.
(Ⅰ)求证: 平面
平面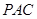 ;
;
(Ⅱ)侧棱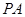 上是否存在点
上是否存在点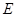 ,使得
,使得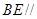 平面
平面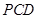 ?若存在,指出点
?若存在,指出点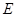 的位置并证明,若不存在,请说明理由;
的位置并证明,若不存在,请说明理由;
(Ⅲ)求二面角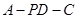 的余弦值.
的余弦值.