观察图1至图4中小黑点的摆放规律,并按照这样的规律继续摆放,记第n个图中小黑点的个数为y。
①填表: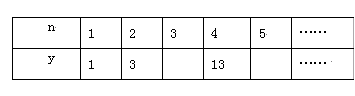
②当n=8时,y=____。
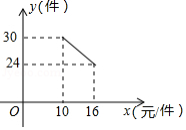
一名在校大学生利用“互联网 ”自主创业,销售一种产品,这种产品的成本价10元 件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元 件,市场调查发现,该产品每天的销售量 (件 与销售价 (元 件)之间的函数关系如图所示.
(1)求 与 之间的函数关系式,并写出自变量 的取值范围;
(2)求每天的销售利润 (元 与销售价 (元 件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
如图, 是 的外接圆, 为直径, 的平分线交 于点 ,过点 作 分别交 、 的延长线于点 、 .
(1)求证: 是 的切线;
(2)若 , ,求 的长度.(结果保留

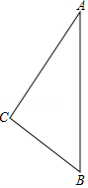
一名徒步爱好者来衡阳旅行,他从宾馆 出发,沿北偏东 的方向行走2000米到达石鼓书院 处,参观后又从 处沿正南方向行走一段距离,到达位于宾馆南偏东 方向的雁峰公园 处,如图所示.
(1)求这名徒步爱好者从石鼓书院走到雁峰公园的途中与宾馆之间的最短距离;
(2)若这名徒步爱好者以100米 分的速度从雁峰公园返回宾馆,那么他在15分钟内能否到达宾馆?
“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,根据测试成绩(成绩都不低于50分)绘制出如图所示的部分频数分布直方图.
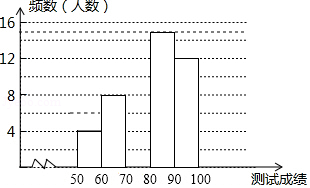
请根据图中信息完成下列各题.
(1)将频数分布直方图补充完整人数;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少;
(3)现将从包括小明和小强在内的4名成绩优异的同学中随机选取两名参加市级比赛,求小明与小强同时被选中的概率.
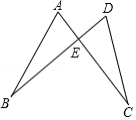
如图,已知线段 , 相交于点 , , .
(1)求证: ;
(2)当 时,求 的长.