设cos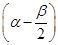 =-
=- ,sin
,sin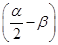 =
= ,其中α∈
,其中α∈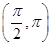 ,β∈
,β∈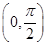 ,求cos
,求cos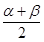 .
.
如图. 直三棱柱ABC —A1B1C1中,A1B1= A1C1,点D、E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.
求证:(1)平面ADE⊥平面BCC1B1
(2)直线A1F∥平面ADE.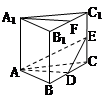
某中学在运动会期间举行定点投篮比赛,规定每人投篮4次,投中一球得2分,没有投中得0分,假设每次投篮投中与否是相互独立的,已知小明每次投篮投中的概率都是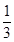 .
.
(1)求小明在投篮过程中直到第三次才投中的概率;
(2)求小明在4次投篮后的总得分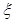 的分布列和期望.
的分布列和期望.
已知函数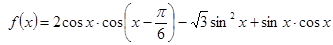
(1)求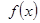 的最小正周期;
的最小正周期;
(2)当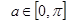 时,若
时,若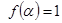 ,求
,求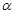 的值.
的值.
各项均不为零的数列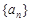 的前
的前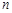 项和为
项和为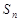 ,且
,且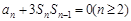 ,
,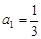 .
.
(1)求数列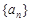 的通项公式
的通项公式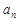 ;
;
(2)若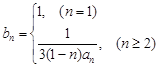 ,设
,设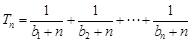 ,若
,若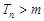 对
对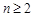 恒成立,求实数
恒成立,求实数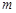 的取值范围.
的取值范围.
已知圆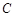 过点
过点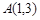 ,
,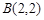 ,并且直线
,并且直线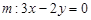 平分圆的面积.
平分圆的面积.
(1)求圆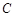 的方程;
的方程;
(2)若过点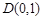 ,且斜率为
,且斜率为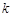 的直线
的直线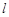 与圆
与圆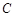 有两个不同的公共点
有两个不同的公共点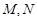 .
.
①求实数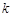 的取值范围;②若
的取值范围;②若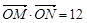 ,求
,求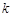 的值.
的值.