(本小题满分13分)已知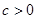 且
且 ,设
,设 :指数函数
:指数函数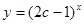 在
在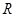 上为减函数,
上为减函数, :不等式
:不等式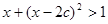 的解集为
的解集为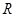 .若
.若 为假,
为假,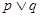 为真,求
为真,求 的取值范围.
的取值范围.
(本小题12分)
某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据
| x |
6 |
8 |
10 |
12 |
| y |
2 |
3 |
5 |
6 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ;
;
(3)试根据(II)求出的线性回归方程,预测记忆力为9的同学的判断力。
(相关公式: )
)
(本小题满分12分)设数列 满足
满足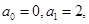 且对一切
且对一切 ,有
,有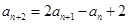
(1)求数列 的通项;
的通项;
(2)设  ,求
,求 的取值范围.
的取值范围.
(本小题满分10分)
已知函数 .
.
(1) 若不等式 的解集为
的解集为 ,求实数
,求实数 的值;
的值;
(2) 在(1)的条件下, 使
使 能成立,求实数a的取值范围.
能成立,求实数a的取值范围.
(本小题满分10分)
在平面直角坐标系 中,直线
中,直线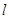 的参数方程为
的参数方程为 (t为参数,α为直线
(t为参数,α为直线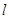 的倾斜角),以原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为
的倾斜角),以原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为 .
.
(1) 若直线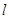 与圆C相切,求
与圆C相切,求 的值;
的值;
(2) 若 直线
直线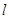 与圆C交与A,B两点,求
与圆C交与A,B两点,求 的值.
的值.
(本小题满分10分)
如图,已知 与圆
与圆 相切于点
相切于点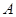 ,经过点
,经过点 的割线
的割线 交圆
交圆 于点
于点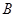 、
、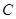 ,
, 的平分线分别交
的平分线分别交 、
、 于点
于点 、
、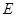 .
.
求证:(1)  .
.
(2) 若 求
求 的值.
的值.