(本小题满分14分)为了解初三学生女生身高情况,某中学对初三女生身高进行了一次抽样调查,根据所得数据整理后列出了频率分布表如下:
组 别 频数 频率
145.5~149.5 1 0.02
149.5~153.5 4 0.08
153.5~157.5 22 0.44
157.5~161.5 13 0.26
161.5~165.5 8 0.16
165.5~169.5 m n
合 计 M N
(1)求出表中所表示的数m,n,M,N分别是多少?
(2)画出频率分布直方图和频率分布折线图.
(3)若要从中再用分层抽样方法抽出10人作进一步调查,则身高在[153.5,161.5)范围内的应抽出多少人?
(4)根据频率分布直方图,分别求出被测女生身高的众数,中位数和平均数?(结果保留一位小数)
在直三棱柱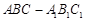 中,
中,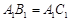 ,
, 分别是棱
分别是棱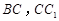 上的点(点
上的点(点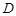 不同于点
不同于点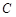 ),且
),且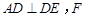 为
为 的中点.
的中点.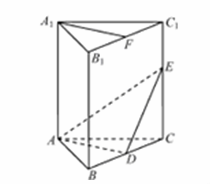
求证:(1)平面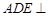 平面
平面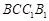 ;
;
(2)直线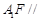 平面
平面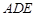 .
.
在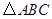 中,角
中,角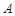 ,
,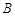 ,
,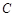 的对边分别为
的对边分别为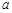 ,
,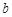 ,
,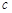 .已知
.已知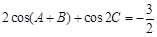 ,
,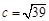 ,且
,且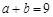 .
.
(Ⅰ)求角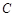 的大小;
的大小;
(Ⅱ)求△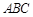 的面积.
的面积.
设函数f(x)=ax-(a+1)ln(x+1),其中a>0.
(1)求f(x)的单调区间;
(2)当x>0时,证明不等式: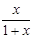 <ln(x+1)<x;
<ln(x+1)<x;
(3)设f(x)的最小值为g(a),证明不等式:-1<ag(a)<0
对n∈N∗不等式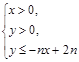 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列(x1,y1),(x2,y2),⋯,(xn,yn),
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列(x1,y1),(x2,y2),⋯,(xn,yn),
求xn,yn;
(2)数列{an}满足a1=x1,且n≥2时an=yn2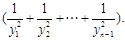 证明:当n≥2时,
证明:当n≥2时,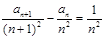 ;
;
(3)在(2)的条件下,试比较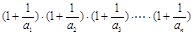 与4的大小关系.
与4的大小关系.
数列{an}满足4a1=1,an-1=[(-1)nan-1-2]an(n≥2),(1)试判断数列{1/an+(-1)n}是否为等比数列,并证明;(2)设an2∙bn=1,求数列{bn}的前n项和Sn.